Question

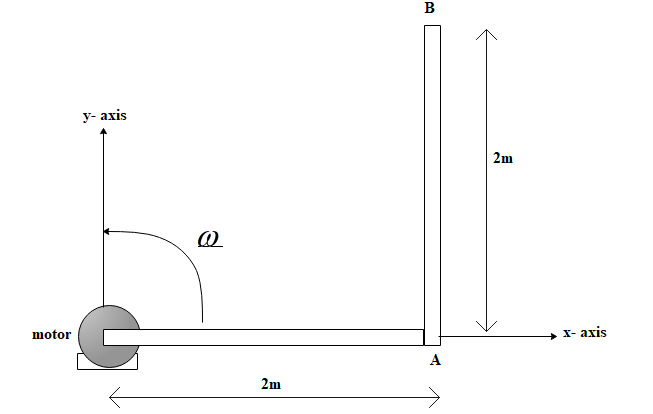
Consider the ‘L’ shaped bar shown in figure. At the instant shown, the bar is rotating at $4rad.{{s}^{-1}}$ and is slowing down at the rate of $2rad.{{s}^{-2}}$.
a).Find the acceleration of point A.
b).Find the relative acceleration ${{a}_{BA}}$ of point B with respect to point A.

Answer 1

Hint: The acceleration at point A has two components. One is the tangential acceleration and the other is the centripetal acceleration. The tangential acceleration of any body is perpendicular to the velocity of the body performing circular motion. The centripetal acceleration is directed towards the center of the circle formed by the circular motion of the body. Thus, we shall find both the components of acceleration and then find the net acceleration.

Complete answer:
Tangential acceleration, ${{a}_{t}}=\alpha r$
Where,
$\alpha =$ angular acceleration of body
$r=$ radius of circular motion
Centripetal acceleration is given by using the equation of motion as:
${{\omega }^{2}}-\omega _{0}^{2}=2r\alpha $
Where,
$\omega =$ final angular velocity of body
${{\omega }_{0}}=$ initial angular velocity of body $=0$ in this case
$r=$ radius of circular motion
$\alpha =$ angular acceleration of body
Thus, centripetal acceleration, ${{a}_{c}}=r{{\omega }^{2}}$
a).Given that for point A, $\omega =4rad.{{s}^{-1}}$, $\alpha =-2rad.{{s}^{-2}}$(as the bar is slowing down) and $r=2m$.
We get,
${{a}_{t}}=\left( -2 \right)2$
$\therefore {{a}_{t}}=-4m{{s}^{-2}}$ …………….. (1)
And ${{a}_{c}}=\left( 2 \right){{\left( 4 \right)}^{2}}$
$\Rightarrow {{a}_{c}}=32m{{s}^{-2}}$ ………………. (2)
Thus, net acceleration, $a=\sqrt{a_{t}^{2}+a_{c}^{2}}$
From (1) and (2), we get
$\begin{align}
  & \Rightarrow a=\sqrt{{{\left( -4 \right)}^{2}}+{{\left( 32 \right)}^{2}}} \\
 & \Rightarrow a=\sqrt{16+1024} \\
 & \Rightarrow a=\sqrt{1040} \\
 & \Rightarrow a=32.25m{{s}^{-2}} \\
\end{align}$
Therefore, the acceleration of point A is $32.25m{{s}^{-2}}$.
Similarly, for point B, we have, $\omega =4rad.{{s}^{-1}}$, $\alpha =-2rad.{{s}^{-2}}$(as the bar is slowing down) and $r=2\sqrt{2}m$.
We get,
${{a}_{t}}=\left( -2 \right)2\sqrt{2}$
$\therefore {{a}_{t}}=-4\sqrt{2}m{{s}^{-2}}$ …………….. (3)
And ${{a}_{c}}=\left( 2\sqrt{2} \right){{\left( 4 \right)}^{2}}$
$\Rightarrow {{a}_{c}}=32\sqrt{2}m{{s}^{-2}}$ ………………. (4)
Thus, net acceleration, $a=\sqrt{a_{t}^{2}+a_{c}^{2}}$
From (3) and (4), we get
$\begin{align}
  & \Rightarrow a=\sqrt{{{\left( -4\sqrt{2} \right)}^{2}}+{{\left( 32\sqrt{2} \right)}^{2}}} \\
 & \Rightarrow a=\sqrt{32+2048} \\
 & \Rightarrow a=\sqrt{2080} \\
 & \Rightarrow a=45.61m{{s}^{-2}} \\
\end{align}$
b).Relative acceleration, ${{a}_{BA}}$, acceleration of B with respect to A is expressed as:
${{a}_{BA}}={{a}_{B}}-{{a}_{A}}$
Where, ${{a}_{B}}=$ acceleration of B and ${{a}_{A}}=$ acceleration of A.
$\begin{align}
  & \Rightarrow {{a}_{BA}}=45.61-32.25 \\
 & \Rightarrow {{a}_{BA}}=13.36m{{s}^{-2}} \\
\end{align}$
Therefore, acceleration of point B with respect to A is $13.36m{{s}^{-2}}$.

Note:
The tangential acceleration is dependent on the radius and angular acceleration of the body whereas the centripetal acceleration is given by applying the equations of motion to the angular motion of the body, that is, we replace the velocity, acceleration and displacement with the angular velocity, angular acceleration and radius in the equations of motion.