
Consider the function $f:R-\{0\}\to R$ defined by $f\left( x \right)=1-{{e}^{\dfrac{1}{x}-1}}$. Which of the following options is correct for the given function $f\left( x \right)$.
(a) One-one into function.
(b) Many-one function.
(c) Onto function.
(d) Not a function.
Answer
583.8k+ views
Hint: We start solving the problem by recalling the definitions of one-one, onto, into, and many-one functions. We then find the derivative of the given and use the property of the increasing function in order to check whether the given function is one-one or not. We then find the range of the given function at all the extremums of the domain to check whether the function is on or not. We use both results to get the desires answer.
Complete step by step answer:
According to the problem, we are given a function $f:R-\{0\}\to R$ defined by $f\left( x \right)=1-{{e}^{\dfrac{1}{x}-1}}$. We need to check which of the following functions are correct.
Let us recall the definitions of one-one, onto, many-one, and into functions.
A function is said to be one-one if the distinct elements of its domain maps to distinct elements of its codomain.
A function is said to be onto function if the range of the given function is equal to its co-domain.
A function is said to be many to one function if has mapped more than one element from domain mapping to at least one of the values of its co-domain.
A function is said to be into a function if the range of the given function is not equal to its co-domain.
Let us differentiate the given function with respect to x on both sides.
So, we get ${{f}^{'}}\left( x \right)=\dfrac{d}{dx}\left( 1-{{e}^{\dfrac{1}{x}-1}} \right)$.
$\Rightarrow {{f}^{'}}\left( x \right)=\dfrac{d}{dx}\left( 1 \right)-\dfrac{d}{dx}\left( {{e}^{\dfrac{1}{x}-1}} \right)$.
\[\Rightarrow {{f}^{'}}\left( x \right)=0-{{e}^{\dfrac{1}{x}-1}}\dfrac{d}{dx}\left( \dfrac{1}{x}-1 \right)\].
\[\Rightarrow {{f}^{'}}\left( x \right)=-{{e}^{\dfrac{1}{x}-1}}\left( \dfrac{d}{dx}\left( \dfrac{1}{x} \right)-\dfrac{d}{dx}\left( 1 \right) \right)\].
\[\Rightarrow {{f}^{'}}\left( x \right)=-{{e}^{\dfrac{1}{x}-1}}\left( \dfrac{-1}{{{x}^{2}}}-0 \right)\].
\[\Rightarrow {{f}^{'}}\left( x \right)=\dfrac{{{e}^{\dfrac{1}{x}-1}}}{{{x}^{2}}}\].
Since the given domain of the function is $R-\left\{ 0 \right\}$, there is no possibility of getting the obtained derivate as undefined. We know that the exponential ${{e}^{ax+b}}$ is always positive. We know that the value of ${{x}^{2}}$ is greater for all values except at $x=0$.
So, we have found ${{f}^{'}}\left( x \right)>0$, for all values of x given in the range. We know that the given function is strictly increasing if its first derivative is greater than zero.
We know that the values of function \[f\left( x \right)\] for every value of x which makes our given function as one-one function ---(1).
Let us find the limits of the function at all the extremums of given domain. i.e., at $x=-\infty $, $x=0$ and $x=\infty $.
So, let us find the limit of function $f\left( x \right)=1-{{e}^{\dfrac{1}{x}-1}}$ at $x=-\infty $.
So, we get $\underset{x\to -\infty }{\mathop{\lim }}\,\left( 1-{{e}^{\dfrac{1}{x}-1}} \right)=1-{{e}^{\dfrac{1}{-\infty }-1}}$.
$\Rightarrow \underset{x\to -\infty }{\mathop{\lim }}\,\left( 1-{{e}^{\dfrac{1}{x}-1}} \right)=1-{{e}^{0-1}}$.
$\Rightarrow \underset{x\to -\infty }{\mathop{\lim }}\,\left( 1-{{e}^{\dfrac{1}{x}-1}} \right)=1-{{e}^{-1}}$.
$\Rightarrow \underset{x\to -\infty }{\mathop{\lim }}\,\left( 1-{{e}^{\dfrac{1}{x}-1}} \right)=1-\dfrac{1}{e}$ ---(2).
Now, let us find the limit of function $f\left( x \right)=1-{{e}^{\dfrac{1}{x}-1}}$ at $x=\infty $.
So, we get $\underset{x\to \infty }{\mathop{\lim }}\,\left( 1-{{e}^{\dfrac{1}{x}-1}} \right)=1-{{e}^{\dfrac{1}{\infty }-1}}$.
$\Rightarrow \underset{x\to \infty }{\mathop{\lim }}\,\left( 1-{{e}^{\dfrac{1}{x}-1}} \right)=1-{{e}^{0-1}}$.
$\Rightarrow \underset{x\to \infty }{\mathop{\lim }}\,\left( 1-{{e}^{\dfrac{1}{x}-1}} \right)=1-{{e}^{-1}}$.
$\Rightarrow \underset{x\to \infty }{\mathop{\lim }}\,\left( 1-{{e}^{\dfrac{1}{x}-1}} \right)=1-\dfrac{1}{e}$ ---(3).
Now, let us find the limit of function $f\left( x \right)=1-{{e}^{\dfrac{1}{x}-1}}$ at $x=0$.
Since 0 is not in the domain of we check left and right-hand limits at $x=0$.
Let us find the left-hand limit at $x=0$.
So, we get $\underset{x\to {{0}^{-}}}{\mathop{\lim }}\,\left( 1-{{e}^{\dfrac{1}{x}-1}} \right)=1-{{e}^{\underset{x\to {{0}^{-}}}{\mathop{\lim }}\,\left( \dfrac{1}{x}-1 \right)}}$.
We know that as x approaches 0 from left sides, the value approaches to negative infinity.
$\Rightarrow \underset{x\to {{0}^{-}}}{\mathop{\lim }}\,\left( 1-{{e}^{\dfrac{1}{x}-1}} \right)=1-{{e}^{-\infty -1}}$.
$\Rightarrow \underset{x\to {{0}^{-}}}{\mathop{\lim }}\,\left( 1-{{e}^{\dfrac{1}{x}-1}} \right)=1-{{e}^{-\infty }}$.
$\Rightarrow \underset{x\to {{0}^{-}}}{\mathop{\lim }}\,\left( 1-{{e}^{\dfrac{1}{x}-1}} \right)=1-0$.
$\Rightarrow \underset{x\to {{0}^{-}}}{\mathop{\lim }}\,\left( 1-{{e}^{\dfrac{1}{x}-1}} \right)=1$ ---(4).
Let us find the right-hand limit at $x=0$.
So, we get $\underset{x\to {{0}^{+}}}{\mathop{\lim }}\,\left( 1-{{e}^{\dfrac{1}{x}-1}} \right)=1-{{e}^{\underset{x\to {{0}^{+}}}{\mathop{\lim }}\,\left( \dfrac{1}{x}-1 \right)}}$.
We know that as x approaches 0 from right sides, the value approaches to positive infinity.
$\Rightarrow \underset{x\to {{0}^{+}}}{\mathop{\lim }}\,\left( 1-{{e}^{\dfrac{1}{x}-1}} \right)=1-{{e}^{+\infty -1}}$.
$\Rightarrow \underset{x\to {{0}^{+}}}{\mathop{\lim }}\,\left( 1-{{e}^{\dfrac{1}{x}-1}} \right)=1-{{e}^{\infty }}$.
$\Rightarrow \underset{x\to {{0}^{+}}}{\mathop{\lim }}\,\left( 1-{{e}^{\dfrac{1}{x}-1}} \right)=1-\infty $.
$\Rightarrow \underset{x\to {{0}^{+}}}{\mathop{\lim }}\,\left( 1-{{e}^{\dfrac{1}{x}-1}} \right)=-\infty $ ---(5).
From equations (2), (3), (4) and (5), we get the range of $f\left( x \right)$ as $\left( -\infty ,0 \right)\cup \left( 0,\dfrac{1}{e} \right)$ which is not equal to the co-domain $R$. So, this makes the function $f\left( x \right)$ as an into function ---(6).
From equations (2) and (6), we have found the function $f\left( x \right)$ as a one-one into function.
∴ The correct option for the given problem is (a).
Note:
We alternatively solve this by drawing the plot $y=1-{{e}^{\dfrac{1}{x}-1}}$ by checking the values of y for every value of x given in the range. The process of solving by the graph is shown as below.
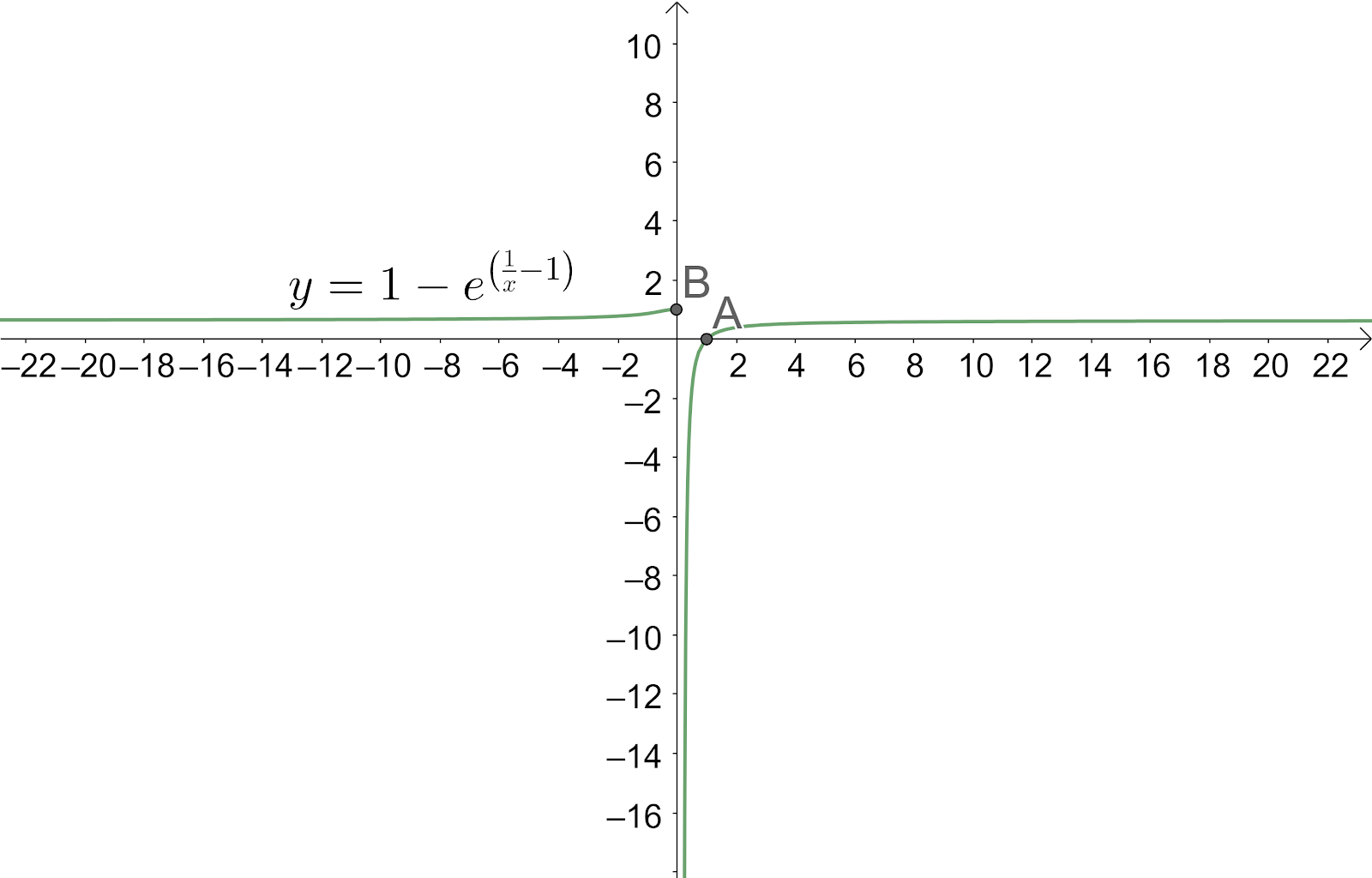
From the graph, we can see that we are getting different values of y for every distinct value of x. We can also see the limits at $x=-\infty $, $x=0$ and $x=\infty $ also the range of y which is not covering the positive values.
Complete step by step answer:
According to the problem, we are given a function $f:R-\{0\}\to R$ defined by $f\left( x \right)=1-{{e}^{\dfrac{1}{x}-1}}$. We need to check which of the following functions are correct.
Let us recall the definitions of one-one, onto, many-one, and into functions.
A function is said to be one-one if the distinct elements of its domain maps to distinct elements of its codomain.
A function is said to be onto function if the range of the given function is equal to its co-domain.
A function is said to be many to one function if has mapped more than one element from domain mapping to at least one of the values of its co-domain.
A function is said to be into a function if the range of the given function is not equal to its co-domain.
Let us differentiate the given function with respect to x on both sides.
So, we get ${{f}^{'}}\left( x \right)=\dfrac{d}{dx}\left( 1-{{e}^{\dfrac{1}{x}-1}} \right)$.
$\Rightarrow {{f}^{'}}\left( x \right)=\dfrac{d}{dx}\left( 1 \right)-\dfrac{d}{dx}\left( {{e}^{\dfrac{1}{x}-1}} \right)$.
\[\Rightarrow {{f}^{'}}\left( x \right)=0-{{e}^{\dfrac{1}{x}-1}}\dfrac{d}{dx}\left( \dfrac{1}{x}-1 \right)\].
\[\Rightarrow {{f}^{'}}\left( x \right)=-{{e}^{\dfrac{1}{x}-1}}\left( \dfrac{d}{dx}\left( \dfrac{1}{x} \right)-\dfrac{d}{dx}\left( 1 \right) \right)\].
\[\Rightarrow {{f}^{'}}\left( x \right)=-{{e}^{\dfrac{1}{x}-1}}\left( \dfrac{-1}{{{x}^{2}}}-0 \right)\].
\[\Rightarrow {{f}^{'}}\left( x \right)=\dfrac{{{e}^{\dfrac{1}{x}-1}}}{{{x}^{2}}}\].
Since the given domain of the function is $R-\left\{ 0 \right\}$, there is no possibility of getting the obtained derivate as undefined. We know that the exponential ${{e}^{ax+b}}$ is always positive. We know that the value of ${{x}^{2}}$ is greater for all values except at $x=0$.
So, we have found ${{f}^{'}}\left( x \right)>0$, for all values of x given in the range. We know that the given function is strictly increasing if its first derivative is greater than zero.
We know that the values of function \[f\left( x \right)\] for every value of x which makes our given function as one-one function ---(1).
Let us find the limits of the function at all the extremums of given domain. i.e., at $x=-\infty $, $x=0$ and $x=\infty $.
So, let us find the limit of function $f\left( x \right)=1-{{e}^{\dfrac{1}{x}-1}}$ at $x=-\infty $.
So, we get $\underset{x\to -\infty }{\mathop{\lim }}\,\left( 1-{{e}^{\dfrac{1}{x}-1}} \right)=1-{{e}^{\dfrac{1}{-\infty }-1}}$.
$\Rightarrow \underset{x\to -\infty }{\mathop{\lim }}\,\left( 1-{{e}^{\dfrac{1}{x}-1}} \right)=1-{{e}^{0-1}}$.
$\Rightarrow \underset{x\to -\infty }{\mathop{\lim }}\,\left( 1-{{e}^{\dfrac{1}{x}-1}} \right)=1-{{e}^{-1}}$.
$\Rightarrow \underset{x\to -\infty }{\mathop{\lim }}\,\left( 1-{{e}^{\dfrac{1}{x}-1}} \right)=1-\dfrac{1}{e}$ ---(2).
Now, let us find the limit of function $f\left( x \right)=1-{{e}^{\dfrac{1}{x}-1}}$ at $x=\infty $.
So, we get $\underset{x\to \infty }{\mathop{\lim }}\,\left( 1-{{e}^{\dfrac{1}{x}-1}} \right)=1-{{e}^{\dfrac{1}{\infty }-1}}$.
$\Rightarrow \underset{x\to \infty }{\mathop{\lim }}\,\left( 1-{{e}^{\dfrac{1}{x}-1}} \right)=1-{{e}^{0-1}}$.
$\Rightarrow \underset{x\to \infty }{\mathop{\lim }}\,\left( 1-{{e}^{\dfrac{1}{x}-1}} \right)=1-{{e}^{-1}}$.
$\Rightarrow \underset{x\to \infty }{\mathop{\lim }}\,\left( 1-{{e}^{\dfrac{1}{x}-1}} \right)=1-\dfrac{1}{e}$ ---(3).
Now, let us find the limit of function $f\left( x \right)=1-{{e}^{\dfrac{1}{x}-1}}$ at $x=0$.
Since 0 is not in the domain of we check left and right-hand limits at $x=0$.
Let us find the left-hand limit at $x=0$.
So, we get $\underset{x\to {{0}^{-}}}{\mathop{\lim }}\,\left( 1-{{e}^{\dfrac{1}{x}-1}} \right)=1-{{e}^{\underset{x\to {{0}^{-}}}{\mathop{\lim }}\,\left( \dfrac{1}{x}-1 \right)}}$.
We know that as x approaches 0 from left sides, the value approaches to negative infinity.
$\Rightarrow \underset{x\to {{0}^{-}}}{\mathop{\lim }}\,\left( 1-{{e}^{\dfrac{1}{x}-1}} \right)=1-{{e}^{-\infty -1}}$.
$\Rightarrow \underset{x\to {{0}^{-}}}{\mathop{\lim }}\,\left( 1-{{e}^{\dfrac{1}{x}-1}} \right)=1-{{e}^{-\infty }}$.
$\Rightarrow \underset{x\to {{0}^{-}}}{\mathop{\lim }}\,\left( 1-{{e}^{\dfrac{1}{x}-1}} \right)=1-0$.
$\Rightarrow \underset{x\to {{0}^{-}}}{\mathop{\lim }}\,\left( 1-{{e}^{\dfrac{1}{x}-1}} \right)=1$ ---(4).
Let us find the right-hand limit at $x=0$.
So, we get $\underset{x\to {{0}^{+}}}{\mathop{\lim }}\,\left( 1-{{e}^{\dfrac{1}{x}-1}} \right)=1-{{e}^{\underset{x\to {{0}^{+}}}{\mathop{\lim }}\,\left( \dfrac{1}{x}-1 \right)}}$.
We know that as x approaches 0 from right sides, the value approaches to positive infinity.
$\Rightarrow \underset{x\to {{0}^{+}}}{\mathop{\lim }}\,\left( 1-{{e}^{\dfrac{1}{x}-1}} \right)=1-{{e}^{+\infty -1}}$.
$\Rightarrow \underset{x\to {{0}^{+}}}{\mathop{\lim }}\,\left( 1-{{e}^{\dfrac{1}{x}-1}} \right)=1-{{e}^{\infty }}$.
$\Rightarrow \underset{x\to {{0}^{+}}}{\mathop{\lim }}\,\left( 1-{{e}^{\dfrac{1}{x}-1}} \right)=1-\infty $.
$\Rightarrow \underset{x\to {{0}^{+}}}{\mathop{\lim }}\,\left( 1-{{e}^{\dfrac{1}{x}-1}} \right)=-\infty $ ---(5).
From equations (2), (3), (4) and (5), we get the range of $f\left( x \right)$ as $\left( -\infty ,0 \right)\cup \left( 0,\dfrac{1}{e} \right)$ which is not equal to the co-domain $R$. So, this makes the function $f\left( x \right)$ as an into function ---(6).
From equations (2) and (6), we have found the function $f\left( x \right)$ as a one-one into function.
∴ The correct option for the given problem is (a).
Note:
We alternatively solve this by drawing the plot $y=1-{{e}^{\dfrac{1}{x}-1}}$ by checking the values of y for every value of x given in the range. The process of solving by the graph is shown as below.

From the graph, we can see that we are getting different values of y for every distinct value of x. We can also see the limits at $x=-\infty $, $x=0$ and $x=\infty $ also the range of y which is not covering the positive values.
Recently Updated Pages
Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Master Class 11 Physics: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Class 11 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Why is there a time difference of about 5 hours between class 10 social science CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE

The draft of the Preamble of the Indian Constitution class 10 social science CBSE

Who gave "Inqilab Zindabad" slogan?

Write a letter to the principal requesting him to grant class 10 english CBSE

Who was Subhash Chandra Bose Why was he called Net class 10 english CBSE




