Question

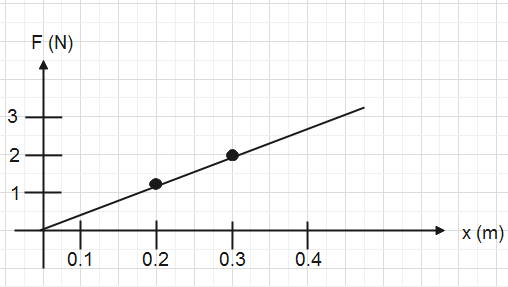
Consider the force vs displacement graph shown above for an ideal spring. Calculate the work done in stretching the spring from $0.2m$ to $0.3m$
(A). $1J$
(B). $10J$
(C). $0.10J$
(D). $0.15J$
(E). $1.5J$

Answer 1

Hint: The graph shows the displacement and the force when a spring is stretched. As the spring is stretched, it moves away from its mean position and hence work is done. The work done to move the spring can be calculated as the area under the graph. The displacement of the spring is the difference in its initial and final position.

Formula used:
$A=\dfrac{1}{2}({{l}_{1}}+{{l}_{2}})\times h$

Complete step by step solution:
The product of force and displacement is known as work done. Its SI unit is joules (J).
When a spring is stretched, it moves away from its mean position which is its equilibrium position. Therefore, work is being done on it which is stored as its potential energy.
The work done is equal to the area covered under the graph
Therefore, the work done while moving the spring from its position at $x=0.2m$ to $x=0.3m$ will be the area of the trapezium. It is given by-
$A=\dfrac{1}{2}({{l}_{1}}+{{l}_{2}})\times h$

From the figure, ${{l}_{1}}=1,\,\,{{l}_{2}}=2$, $h=0.3-0.2=0.1$
Now we substitute given values in the above equation,
$\begin{align}
  & W=\dfrac{1}{2}(1+2)\times 0.1 \\
 & \Rightarrow W=0.15J \\
\end{align}$
The work done to stretch the spring is $0.15J$.
Therefore, the work done in stretching the spring from $0.2m$ to $0.3m$ is $0.15J$.
Hence, the correct option is (D).

Note: The force is the restoring force which is developed in the spring as it is stretched farther from its mean position. The force developed per unit displacement is known as the spring constant. The motion of the spring about its mean position follows simple harmonic motion. As we go away from the mean position, the potential energy of the spring increases. Its potential energy is highest at the extreme positions and kinetic energy is highest at its mean position.