Question

Consider the following statements relating to 3 lines $L_1$​, $L_2$​ and $L_3$​ in the same plane
(1). If $L_2$​ and $L_3$​ are both parallel to $L_1$​, then they are parallel to each other.
(2). If $L_2$​ and $L_3$​ are both perpendicular to $L_1$​, then they are parallel to each other.
(3). If the acute angle between $L_1$​ and $L_2$​ is equal to the acute angle between $L_1$​ and $L_3$​, then $L_2$​ is parallel to $L_3$​.
Of these statements:
(A) (1) and (2) are correct.
(B) (1) and (3) are correct.
(C) (2) and (3) are correct.
(D) (1), (2) and (2) are correct.

Answer 1

Hint: In order to solve this question we need to consider the contradiction method . This method is very useful when we have to prove the statement given in the question . We make the assumption that the given statement is false and it gets proven when the result comes just opposite . We will also apply some axioms and properties like the sum of angles of a triangle is and if A=B, B=C then definitely A=C . By using these little properties we are going to solve this question ahead .

Complete step-by-step answer:
1 => If $L_2$ and $L_3$ are both parallel to $L_1$, then they are parallel to each other.
This is true. We can prove this using contradiction, i.e., let $L_2$ and $L_3$ are not parallel.
Now, we know that if two lines in a plane are not parallel, then they intersect each other at some point.
Therefore, $L_2$ and $L_3$ intersect each other at some point.
Since, $L_1$ is parallel to $L_2$, then $L_1$ must also intersect $L_3$. But, we have already assumed $L_1$ and $L_3$ are parallel.

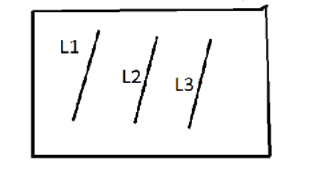
This implies that our assumption that $L_2$ and $L_3$ are not parallel is incorrect.
Hence, $L_2$ and $L_3$ are parallel to each other.

2 => If $L_2$ and $L_3$ are both perpendicular to $L_1$, then they are parallel to each other.
This is true. We can prove this using contradiction, i.e., let $L_2$ and $L_3$ are not parallel.

If $L_2$ and $L_3$ are not parallel, it implies that they intersect at some point. Let this point be A.
Also, $L_2$ and $L_3$ are both perpendicular to $L_1$, which implies that $L_2$ and $L_3$ intersect $L_1$ at some point. Let these points be B and C respectively.

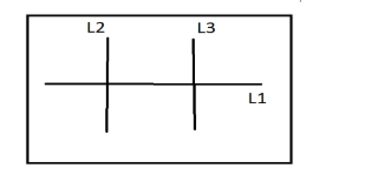
Now, we know that the sum of angles of a triangle is \[{180^ \circ }.\]We can use this fact to calculate the angle \[\angle BAC\].
\[\angle BAC{\text{ }} + \angle ABC{\text{ }} + \angle ACB{\text{ }} = {\text{ }}{180^ \circ }\]
Since, $L_2$ and $L_3$ are both perpendicular to $L_1$,
\[\angle ABC{\text{ }} = {\text{ }}{90^ \circ }{\text{ }}and\angle ACB{\text{ }} = {\text{ }}{90^ \circ }.\]
Using the above fact, we can determine the angle between $L_2$ and $L_3$, i.e,
\[\angle BAC{\text{ }} = {\text{ }}{180^ \circ }{\text{ }} - {\text{ }}{90^ \circ }{\text{ }} - {\text{ }}{90^ \circ }\]
\[\angle BAC{\text{ }} = {\text{ }}{0^ \circ }\]
This contradicts our assumption that $L_2$ and $L_3$ are not parallel.
Hence, $L_2$ and $L_3$ are parallel to each other.


3 => If the acute angle between $L_1$ and $L_2$ is equal to the acute angle between $L_1$ and $L_3$, then $L_2$ is parallel to $L_3$.
This is true. We can prove this by the concept of corresponding angles.

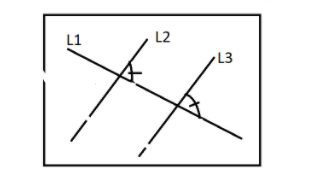
Let the angle between $L_1$ and $L_2$ be \[{30^ \circ }.\] .This implies that, angle between $L_1$ and $L_3$ will also be \[{30^ \circ }.\]. Because $L_2$ and $L_3$ are parallel and the corresponding angle between them is the same \[{30^ \circ }.\] We can draw such lines in such a way that $L_1$ is an angle bisector of the angle between $L_2$ and $L_3$ .
Therefore, option D is correct .
So, the correct answer is “Option D”.

Note: Always try to understand the mathematical statement carefully and keep things distinct .
Whenever there is a statement proving type questions , try to use a contradiction method .
Remember the properties and apply appropriately .
Choose the options wisely , it's better to break the question and then solve part by part .
Cross check the answer and always keep the final answer simplified .