Question

Consider the following relations
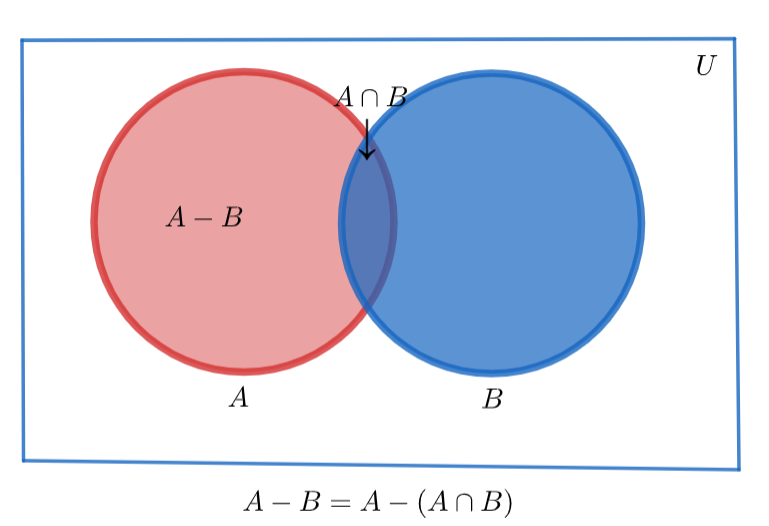
1. \[A-B=A-\left( A\bigcap B \right)\]
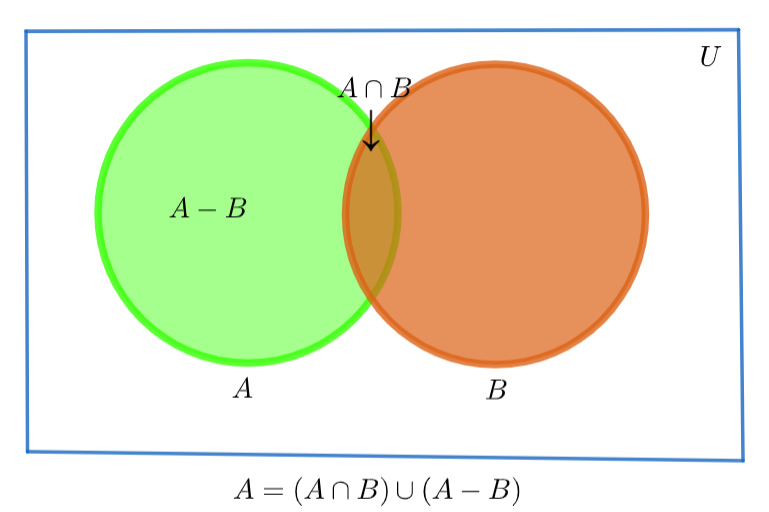
2. \[A=\left( A\bigcap B \right)\bigcup \left( A-B \right)\]
3. \[A-\left( B\bigcup C \right)=\left( A-B \right)\bigcup \left( A-C \right)\]
Which of these is/are correct?

Answer 1

Hint: In this type of question we have to use the concept of set theory. In case of set theory we know that, if \[A\And B\] are any two sets then, \[A-B=A\bigcap B'\] where \[B'\] is the complement of set \[B\]. Also we know that if \[A\] is a set then \[A\bigcap A'=\varphi \] and \[A\bigcup A'=U\] where \[\varphi \] represents empty set and \[U\] represents universal set. By De-Morgan’s Law we have, \[\left( A\bigcap B \right)'=\left( A'\bigcup B' \right)\] and by distributive law \[A\bigcap \left( B\bigcup C \right)=\left( A\bigcap B \right)\bigcup \left( A\bigcap C \right)\]. Here we consider each of the statements separately and then we check whether it is correct or not.

Complete step by step answer:
Now we have given
1. \[A-B=A-\left( A\bigcap B \right)\]
2. \[A=\left( A\bigcap B \right)\bigcup \left( A-B \right)\]
3. \[A-\left( B\bigcup C \right)=\left( A-B \right)\bigcup \left( A-C \right)\]
And we have to check which statement is/are correct
Let us consider the each statement one by one and check whether they are correct or not
Let us start with the first statement
1. \[A-B=A-\left( A\bigcap B \right)\]
\[\Rightarrow R.H.S.=A-\left( A\bigcap B \right)\]
As we know, \[A-B=A\bigcap B'\] where \[B'\] is the complement of the set \[B\].
\[\Rightarrow R.H.S.=A\bigcap \left( A\bigcap B \right)'\]
Now by De-Morgan’s theorem we have, \[\left( A\bigcap B \right)'=\left( A'\bigcup B' \right)\]
\[\Rightarrow R.H.S.=A\bigcap \left( A'\bigcup B' \right)\]
By using distributive law i.e. \[A\bigcap \left( B\bigcup C \right)=\left( A\bigcap B \right)\bigcup \left( A\bigcap C \right)\] we can write,
\[\Rightarrow R.H.S.=\left( A\bigcap A' \right)\bigcup \left( A\bigcap B' \right)\]
Now as we know that \[A\bigcap A'=\varphi \] we get,
\[\begin{align}
  & \Rightarrow R.H.S.=\varphi \bigcup \left( A\bigcap B' \right) \\
 & \Rightarrow R.H.S=\left( A\bigcap B' \right) \\
\end{align}\]
Again we will use \[A-B=A\bigcap B'\] and hence we get,
\[\Rightarrow R.H.S.=A-B\]
But we have given
\[\Rightarrow L.H.S.=A-B\]
\[\Rightarrow L.H.S.=R.H.S.\]
\[\Rightarrow A-B=A-\left( A\bigcap B \right)\]
Hence, statement 1 is correct.

Now, let us consider the second statement
2. \[A=\left( A\bigcap B \right)\bigcup \left( A-B \right)\]
To check whether this statement is correct or not let us start with its R.H.S.
\[\Rightarrow R.H.S.=\left( A\bigcap B \right)\bigcup \left( A-B \right)\]
Now as we have \[A-B=A\bigcap B'\] we can rewrite the above expression as
\[\Rightarrow R.H.S.=\left( A\bigcap B \right)\bigcup \left( A\bigcap B' \right)\]
Now we will use distributive law i.e. \[A\bigcap \left( B\bigcup C \right)=\left( A\bigcap B \right)\bigcup \left( A\bigcap C \right)\]
\[\Rightarrow R.H.S.=A\bigcap \left( B\bigcup B' \right)\]
But as we know that if \[B\] is any set then \[\left( B\bigcup B' \right)=U\] where \[U\] is the universal set
\[\begin{align}
  & \Rightarrow R.H.S.=A\bigcap U \\
 & \Rightarrow R.H.S.=A \\
\end{align}\]
By given
\[\Rightarrow L.H.S.=A\]
\[\Rightarrow L.H.S.=R.H.S.\]
\[\Rightarrow A=\left( A\bigcap B \right)\bigcup \left( A-B \right)\]
Hence, the second statement is also correct.

Now, we will check for the third statement
3. \[A-\left( B\bigcup C \right)=\left( A-B \right)\bigcup \left( A-C \right)\]
In this case we will simplify L.H.S. and R.H.S separately
So let us consider L.H.S.
\[\begin{align}
  & \Rightarrow L.H.S=A-\left( B\bigcup C \right) \\
 & \Rightarrow L.H.S=A\bigcap \left( B\bigcup C \right)'\cdots \cdots \cdots \left\{ A-B=A\bigcap B' \right\} \\
 & \Rightarrow L.H.S=A\bigcap \left( B'\bigcap C' \right)\cdots \cdots \cdots \left( DeMorgan's\text{ }Law \right) \\
 & \Rightarrow L.H.S.=\left( A\bigcap B' \right)\bigcap \left( A\bigcap C' \right)\cdots \cdots \cdots \left( Distributive\text{ }\Pr operty \right) \\
\end{align}\]
Now we will simplify R.H.S.
\[\begin{align}
  & \Rightarrow R.H.S.=\left( A-B \right)\bigcup \left( A-C \right) \\
 & \Rightarrow R.H.S=\left( A\bigcap B' \right)\bigcup \left( A\bigcap C' \right)\cdots \cdots \cdots \left\{ A-B=A\bigcap B' \right\} \\
\end{align}\]
Here we can easily observe that,
\[\Rightarrow L.H.S.\ne R.H.S.\]
Hence, statement 3 is incorrect
\[\Rightarrow A-\left( B\bigcup C \right)\ne \left( A-B \right)\bigcup \left( A-C \right)\]
Thus, we can say that statements 1 and 2 are correct statements.

Note: In this type of question students must be clear with the properties of set theory. Also students have to remember De-Morgan’s Law and Distributive property of set theory. Students have to note that though the third statement is incorrect the corresponding correct statement is \[A-\left( B\bigcup C \right)=\left( A-B \right)\bigcap \left( A-C \right)\].