Question

Consider the following parallelograms. Find the values of the unknowns $x,y,z$

Answer 1

Hint: Use the properties of parallelogram such that opposite angles are equal, adjacent angles are supplementary and properties of parallel lines and intersecting lines to find the value of $x,y,z$ in all the given figure.

Complete step by step Answer:

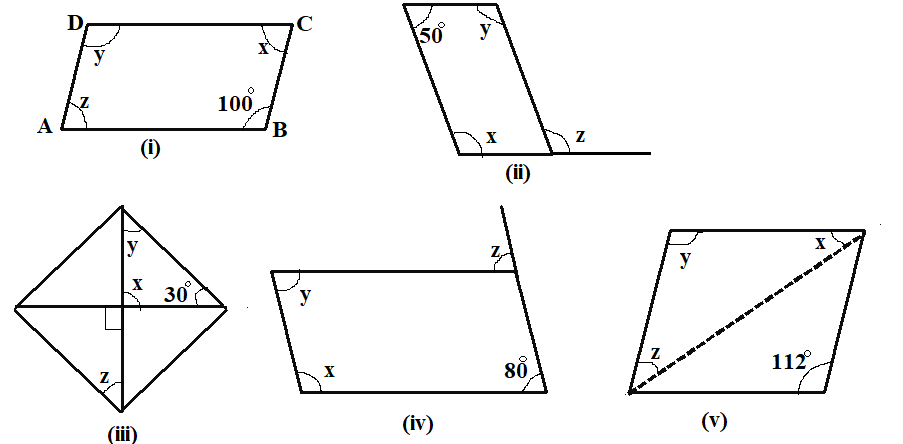
In the first part, we have a parallelogram ABCD.

Now, we know that the sum of adjacent angles in a parallelogram is ${180^ \circ }$
Then, from the above figure, $\angle B + \angle C = {180^ \circ }$. Also, the value of the $\angle B$ is ${100^ \circ }$
On substituting the given values, we get,
 $
  {100^ \circ } + x = {180^ \circ } \\
   \Rightarrow x = {80^ \circ } \\
$
In a parallelogram, opposite angles are equal.
Therefore, we have $y = {100^ \circ }$ and $z = {80^ \circ }$
Now, let us find the values of $x,y,z$ in the figure (ii)

Again, we can use the property of parallelogram that the sum of the adjacent angles of the parallelogram is ${180^ \circ }$
Then, we have
$
  {50^ \circ } + x = {180^ \circ } \\
   \Rightarrow x = {180^ \circ } - {50^ \circ } \\
   \Rightarrow x = {130^ \circ } \\
$
Also, opposite angles of a parallelogram are equal.
Then , \[y = {130^ \circ }\]
In a parallelogram, the opposite sides are parallel to each other, then we can see that $y$ and $z$ are alternate interior angles.
Hence, \[z = {130^ \circ }\]
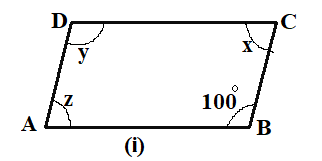
Let us now find the value of $x,y,z$ in the figure (iii)

Here, we can see that $x = {90^ \circ }$ using the property of vertically opposite angles.
Now, in $\vartriangle AEC$, the sum of all the angles is ${180^ \circ }$
That is, $x + y + {30^ \circ } = {180^ \circ }$
On substituting the value of $x = {90^ \circ }$, we get
$
  {90^ \circ } + y + {30^ \circ } = {180^ \circ } \\
   \Rightarrow y + {120^ \circ } = {180^ \circ } \\
   \Rightarrow y = {60^ \circ } \\
 $
Also, $z = y$ as both are alternate interior angles.
Hence, $z = {60^ \circ }$
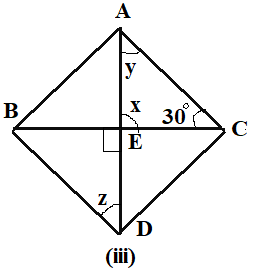
We now will find the values of \[x,y,z\] in figure (iv)

In a parallelogram, opposite angles are equal. Then, we can say that $y = {80^ \circ }$
Also, the sum of adjacent angles in a parallelogram are supplementary.
Then,
$
  x + {80^ \circ } = {180^ \circ } \\
   \Rightarrow x = {100^ \circ } \\
$
It is known that the opposite sides in a parallelogram are equal.
Thus, $z = {80^ \circ }$ using the property of corresponding angles.
We now will find the values of \[x,y,z\] in figure (v)

In a parallelogram, opposite angles are equal. Then, we can say that $y = {112^ \circ }$
We know that the diagonal bisect the angles. Then, $x = z$
Consider the triangle $\vartriangle BAC$, the sum of all the angles of a triangle is ${180^ \circ }$
Then, $x + y + z = {180^ \circ }$
On substituting the values, we get,
$
  x + {112^ \circ } + x = {180^ \circ } \\
   \Rightarrow 2x + {112^ \circ } = {180^ \circ } \\
   \Rightarrow 2x = {180^ \circ } - {112^ \circ } \\
   \Rightarrow 2x = {68^ \circ } \\
   \Rightarrow x = {34^ \circ } \\
$
Then, $z = {34^ \circ }$

Note: A parallelogram is a quadrilateral which two pairs of parallel and equal sides. Opposite angles of a parallelogram are equal. The angle between perpendicular lines is 90 degrees. Students should know all the properties of a parallelogram to do these types of questions.