Question

Consider the following figure where ${E_1} = 8.4{\text{V}}$ and ${E_2} = 4.2{\text{V}}$.

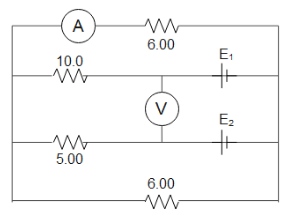
What are the expected reading of the ideal ammeter and voltmeter?

Answer 1

Hint: We are given a circuit consisting of resistors and two cells and we are required to find the reading of the ammeter which is the measure of the current flowing through the circuit and the reading of the voltmeter which is the measure of the potential difference between the two points where the voltmeter is connected.

Complete step by step answer:
Given ${E_1} = 8.4{\text{V}}$ and ${E_2} = 4.2{\text{V}}$
To find the required values we need to label the current and the voltages across the resistors in the given diagram.

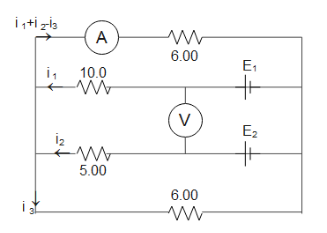
Applying Kirchhoff’s law in the upper loop we get
$ - 10{i_1} - 6({i_1} + {i_2} - {i_3}) + 8.4 = 0$
$\Rightarrow - 16{i_1} - 6{i_2} + 6{i_3} + 8.4 = 0$
Further simplifying the equation we get,
$16{i_1} - 6{i_2} - 6{i_3} = 8.4 - - - (1)$
Applying Kirchhoff’s law in the middle loop we get
$ - 5{i_2} + 10{i_1} - 4.2 + 8.4 = 0$
$\Rightarrow 10{i_1} - 5{i_2} = - 4.2 - - - (2)$
And lastly applying Kirchhoff’s law in the bottom loop we get
$ - 5{i_2} - 6{i_3} + 4.2 = 0$
$\Rightarrow 5{i_2} + 6{i_3} = 4.2 - - - (3)$
Using the substitution method we will find the value of the variables
Firstly from equation (2), we get ${i_2} = \dfrac{{10{i_1} + 4.2}}{5} - - - (4)$
And from equation (3) we get ${i_3} = \dfrac{{ - 5{i_2} + 4.2}}{6} - - - (5)$

Substituting the value in equation (1) we get
$16{i_1} - \dfrac{6}{5}(10{i_1} + 4.2) - \dfrac{6}{6}( - 5{i_2} + 4.2) = 8.4$
Solving the equation we get
$16{i_1} - 12{i_1} - \dfrac{{6 \times 4.2}}{5} + 5\left( {\dfrac{{10{i_1} + 4.2}}{5}} \right) - 4.2 = 8.4$
$\Rightarrow 14{i_1} = 8.4 + \dfrac{{6 \times 4.2}}{5}$
Making current the subject of the equation
${i_1} = \dfrac{{67.2}}{{70}} = 0.96{\text{A}}$
Substituting the above value in equation 4) we get
${i_2} = \dfrac{{10\left( {\dfrac{{67.2}}{{70}}} \right) + 4.2}}{5} = 2.76{\text{A}}$
And substituting the value in equation 5) we get
${i_3} = \dfrac{{ - 5(2.76) + 4.2}}{6} = - 1.6{\text{A}}$
Now the reading of the ammeter would be ${i_1} + {i_2} - {i_3} = 5.32{\text{A}}$.
The reading of the voltmeter would be $8.4 - 4.2 = 4.2{\text{V}}$.

Note: We used Kirchhoff’s voltage law to find the relation between various currents and the potential difference in the different loops. According to Kirchhoff’s voltage law, the voltage around a loop equals the sum of every potential drop in the same loop for any closed network and also equals zero. And we also used Kirchhoff’s current law to determine the current through each branch and the law says that the total current entering a junction or node is equal to the total current leaving the node or junction.