Question

Consider the circuit shown in the figure. The current $I_3$ is equal to:

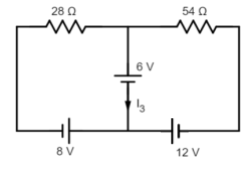
A). $5\;A$
B). $3\;A$
C). $-3\;A$
D). $-\dfrac{5}{6}\;A$

Answer 1

Hint: Use Kirchhoff’s Current Law to obtain an expression for $I_3$ in terms of the currents flowing across the $8\;V$ and $12\;V$ supply voltages. Then, divide the circuit into two independent loops and apply Kirchhoff’s Voltage Law to each to arrive at the magnitude of currents across the before mentioned supply voltages. Use Ohm’s Law to find the voltage drops across the resistance elements. Then plug the values of these currents into the Current law expression to arrive at an appropriate value for $I_3$.
Formula Used:
Kirchhoff’s Current Law (KCL): $I_{entering} + I_{exiting} = 0$
Kirchhoff’s Voltage Law (KVL): $\Sigma V =0$
Ohm’s law: $V=IR$

Complete step-by-step solution:
The only tools we need to solve this problem are Kirchhoff’s Current Law and Kirchhoff’s Voltage Law.
Kirchhoff’s Current Law (KCL) suggests that the algebraic sum of currents entering a node in a circuit will be equal to the sum of currents leaving the node.
Kirchhoff’s Voltage Law (KVL) suggests that the sum of all voltages around any closed loop in a circuit must be equal to zero.

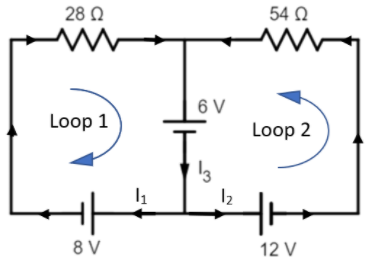
From the above diagram, we see that we can apply KCL to the node in the lower part of the circuit that is in between the $8\;V$ and $12\;V$ batteries.
Applying KCL at this node, we get:
$I_3 = I_1 +I_2$
We thus need to find $I_1$ and $I_2$
Now, our circuit can be deconstructed into two loops as shown in the figure. Since our circuit consists of two independent closed loops, let us apply KVL to each and see how it goes from there.
In Loop 1, the $28\Omega$ resistor is powered by the current $I_1$ from the $8\;V$ supply.
Therefore, the voltage drop across this resistor will be $V = RI = 28I_1$
Now, applying KVL to Loop 1, we get:
$28I_1 + 6 +8 = 0 \Rightarrow 28I_1 = -6-8 = -14$
$\Rightarrow I_1 = \dfrac{-14}{28} = -\dfrac{1}{2}\;A$
Similarly, in Loop 2, the $54\Omega$ resistor is powered by the current $I_2$ from the $12\;V$ supply.
Therefore, the voltage drop across this resistor will be $V = RI = 54I_2$
Now, applying KVL to Loop 2, we get:
$54I_2 + 6 +12 = 0 \Rightarrow 54I_2 = -6-12 = -18$
$\Rightarrow I_2 = \dfrac{-18}{54} = -\dfrac{1}{3}\;A$
From the KCL equation, and the value of $I_1$ and $I_2$ that we found, we can now calculate $I_3$:
$I_3 = I_1 +I_2 = -\dfrac{1}{2} + \left(-\dfrac{1}{3}\right) = \dfrac{-3-2}{6} = -\dfrac{5}{6}\;A$. Therefore, the correct choice would be D. $-\dfrac{5}{6}\;A$

Note: Though we looked at KCL and KVL from a quantitative perspective, it is important to understand what they mean in a physical sense.
KCL signifies conservation of charge since the law basically suggests that the sum of currents entering a node must be equal to the sum of currents leaving the node, which means that electric charges are neither ambiguously lost nor mysteriously added but remains the same in an isolated system.
KVL signifies conservation of energy since the total energy in a system remains constant, though it may be transferred between components of the system in the form of electric potential and current.