Question

Consider the circuit below where all resistor is of $1\;k\Omega $. If a current of magnitude $1\;mA$ flows through the resistor marked $x\;$. What is the potential difference measured between points $P\;$ and $Q\;$:-

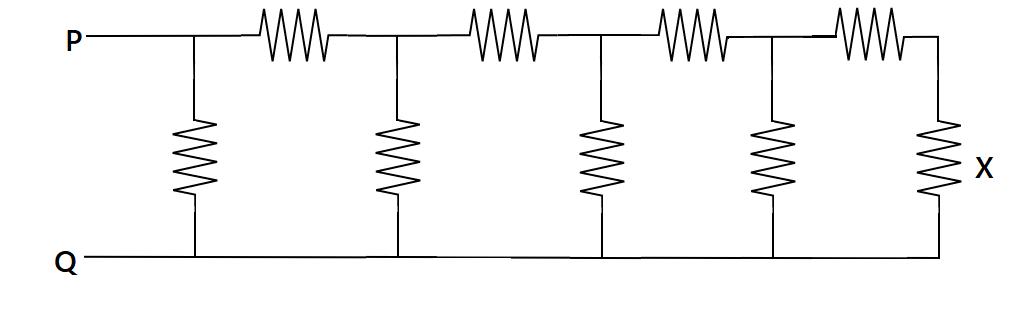
A. $21\;V$
B. $68\;V$
C. $55\;V$
D. $34\;V$

Answer 1

Hint: To solve this question we will use ohm's law. As ohm's law states that the current passing through the conductor is directly proportional to the potential difference across the conductor at constant temperature and pressure. We will use the series and parallel connection properties of the resistance to evaluating the resistance of the given circuit.

Formula used: Ohms law of a current passing through any conductor
$V = iR$

Complete step by step answer:

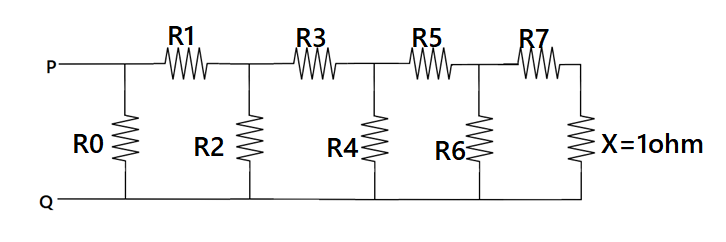
Here it is given that all the resistors which are connected in the circuit are of the same resistance. Hence
$ \Rightarrow {R_0} = {R_1} = {R_2} = {R_3} = {R_4} = {R_5} = {R_6} = {R_7} = {R_8}$
Now according to ohm's law
$ \Rightarrow {i_6}{R_6} = {i_7}\left( {{R_7} + X} \right)$
As given that the current through the ${i_7} = 1mA$, and taking $X = {R_7} = {R_6} = k$
$ \Rightarrow {i_6}{R_6} = \left( {{R_7} + X} \right)$
$ \Rightarrow {i_6}k = 2k$
Hence the current obtained through ${i_6} = 2\;mA$.
Now applying Kirchoff's junction law
$ \Rightarrow {i_5} = {i_6} + {i_7}$
$ \Rightarrow {i_5} = 3\;mA$
Now as we can see that resistance ${R_7}$ and $X$ are in series then it is given as shown

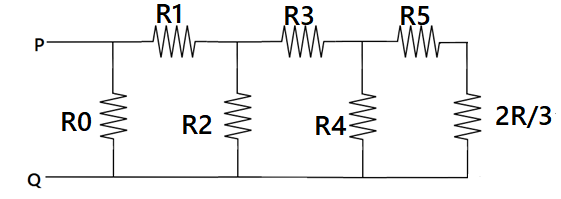
Now their equivalent resistance is parallel to the ${R_6}$, hence now again using ohms law
$ \Rightarrow {i_4}{R_4} = {i_5}\left( {{R_5} + \dfrac{{2R}}{3}} \right)$
Substituting that ${R_4} = {R_5} = R$
$ \Rightarrow {i_4}R = 3 \times \left( {R + \dfrac{{2R}}{3}} \right)$
Now the current through the resistance ${R_5}$ is given as
$ \Rightarrow {i_4}R = 3 \times \left( {\dfrac{{5R}}{3}} \right)$
$ \Rightarrow {i_4} = 5\;mA$
Now again apply Kirchoff junction law we get
$ \Rightarrow {i_3} = {i_4} + {i_5}$
$ \Rightarrow {i_3} = 8\;mA$
Now we can see that ${R_5}$ and $\dfrac{{2R}}{3}$ are in series connection and their equivalent resistance obtained is parallel to the ${R_4}$, hence overall equivalent resistance is given as $\dfrac{{5R}}{8}$

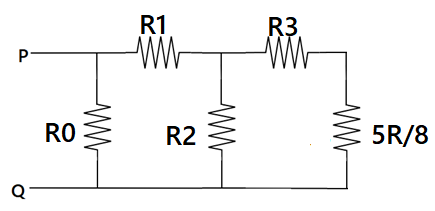
Now according to ohm's law
$ \Rightarrow {i_2}{R_2} = {i_3}\left( {{R_4} + \dfrac{{5R}}{8}} \right)$
Substituting that ${R_2} = {R_3} = R$
$ \Rightarrow {i_2}R = 8\left( {R + \dfrac{{5R}}{8}} \right)$
Now the current through the resistance ${R_2}$ is given as
$ \Rightarrow {i_2}R = 8 \times \left( {\dfrac{{13R}}{8}} \right)$
$ \Rightarrow {i_2} = 13\;mA$
Now again apply Kirchoff junction law we get
$ \Rightarrow {i_1} = {i_2} + {i_3}$
$ \Rightarrow {i_1} = 21\;mA$
Now the resistance ${R_3}$ and $\dfrac{{5R}}{8}$ are in series and the resistance ${R_2}$and equivalent resistance are parallel, hence its overall equivalence resistance of the circuit is given as $\dfrac{{13R}}{{21}}$.

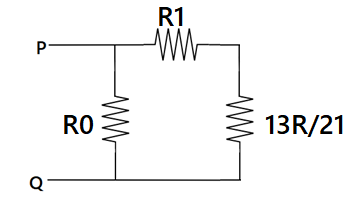
Now again according to ohm's law
$ \Rightarrow {i_0}{R_0} = {i_1}\left( {R + \dfrac{{13R}}{{21}}} \right)$
$ \Rightarrow {i_0}R = 21\left( {R + \dfrac{{13R}}{{21}}} \right)$
$ \Rightarrow {i_0} = 34\;mA$
Now we have total current flowing in the circuit as
$ \Rightarrow {i_T} = {i_0} + i$
$ \Rightarrow {i_T} = 34 + 21$
$\therefore {i_T} = 55\;mA$
Now we have to evaluate the potential difference across the given ends $P\;Q$ as
$ \Rightarrow {V_{PQ}} = {i_0}R$
$ \Rightarrow {V_{PQ}} = 34 \times 10 \times 10 \times 1$
$\therefore {V_{PQ}} = 34\;V$
Hence, option (D) is the correct option.

Note: Here, in this question we have used Kirchhoff’s junction law. It should be noted that if the current is coming towards the junction then we have to consider the current as positive while if currents are distributing and going from the junction then we have to consider the negative sign.