Question

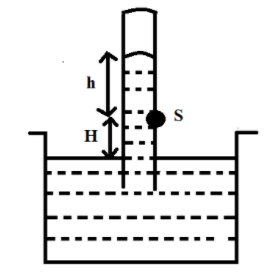
Consider the barometer shown in the figure. Density of mercury is $\rho $. A small hole is made at point S as shown. The mercury comes out from this hole with a speed equal to
$A)\sqrt{2gh}$
$B)\sqrt{2gH}$
$C)\sqrt{2g(H-h)}$
$D)$ none of these

Answer 1

Hint: Bernoulli’s principle is applied to the top surface of the mercury level inside the barometer as well as the surface of a small hole, inside the barometer. We equate the incompressible flow equations of both these surfaces to determine the speed of flow of mercury through the hole, inside the barometer.

Formula used:
$\dfrac{{{v}^{2}}}{2}+gz+\dfrac{p}{\rho }=cons\tan t$

Complete answer:
We know that barometers are used to measure atmospheric pressure. The fluid used in barometers is usually chosen to be incompressible. Mercury is a good example for such a type of fluid. To calculate the atmospheric pressure, a barometer is dipped in this fluid, which is filled in a reservoir. If we make a small hole in the barometer as shown in the question diagram, it is seen that mercury flows through this small hole with a particular velocity. We are required to find this velocity.
Bernoulli’s principle states that an increase in speed of a fluid occurs simultaneously with a decrease in the fluid’s potential energy. Mathematically, Bernoulli’s principle for an incompressible fluid is given by
$\dfrac{{{v}^{2}}}{2}+gz+\dfrac{p}{\rho }=cons\tan t$
where
$v$ is the speed of fluid flow at a point
$g$ is the acceleration due to gravity
$z$ is the height of the considered point from a reference surface
$p$ is the pressure at the considered point
$\rho $ is the density of the fluid
Let this be equation1. Equation 1 is also called an incompressible flow equation, since the fluid used is incompressible.

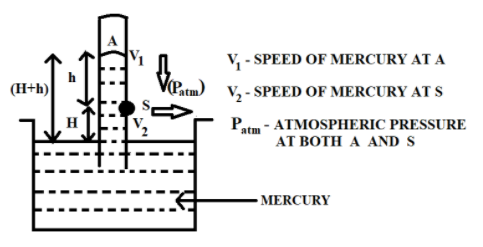
Now, let us apply Bernoulli’s principle to two points, namely A and S, in the figure given above. Clearly, point A is the topmost point of the surface of mercury level inside the barometer and point B is considered on a surface just after the small hole in the barometer. Incompressible fluid equation at point A is given by
$\dfrac{{{v}_{1}}^{2}}{2}+g(H+h)+\dfrac{{{P}_{atm}}}{\rho }=cons\tan t$
where
${{v}_{1}}$ is the speed of mercury at point A
$g$ is the acceleration due to gravity
$(H+h)$ is the height of mercury column from the surface of mercury in the reservoir
${{P}_{atm}}$ is the atmospheric pressure, as measured by the barometer
$\rho $ is the density of mercury
Let this be equation 2.
Incompressible flow equation at point B is given by
$\dfrac{{{v}_{2}}^{2}}{2}+g(H)+\dfrac{{{P}_{atm}}}{\rho }=cons\tan t$
where
${{v}_{2}}$ is the speed of mercury at point S
$g$ is the acceleration due to gravity
$H$ is the height of hole from the surface of mercury in the reservoir
${{P}_{atm}}$ is the atmospheric pressure, as measured by the barometer
$\rho $ is the density of mercury
Let this be equation 3.
It is to be noted that pressure at point A as well as point S is considered to be the same. A barometer is used to measure atmospheric pressure. Even though there might be slight changes in pressures at point A and point S, these are neglected and both are considered to be equal to atmospheric pressure$({{P}_{atm}})$.
Now, according to Bernoulli’s principle, equation 2 and equation 3 are equal. Therefore, we have
$\dfrac{{{v}_{1}}^{2}}{2}+g(H+h)+\dfrac{{{P}_{atm}}}{\rho }=\dfrac{{{v}_{2}}^{2}}{2}+g(H)+\dfrac{{{P}_{atm}}}{\rho }$
Simplifying the above equation, we have
$\dfrac{{{v}_{1}}^{2}}{2}+g(H+h)+\dfrac{{{P}_{atm}}}{\rho }=\dfrac{{{v}_{2}}^{2}}{2}+g(H)+\dfrac{{{P}_{atm}}}{\rho }\Rightarrow \dfrac{{{v}_{1}}^{2}}{2}+g(H+h)=\dfrac{{{v}_{2}}^{2}}{2}+g(H)\Rightarrow {{v}_{2}}^{2}-{{v}_{1}}^{2}=2gh$
Let this be equation 4.
Since the topmost surface of mercury level inside the barometer has a high horizontal cross-sectional area when compared to that of the small hole in the barometer, the velocity at point A is considered to be negligible. Therefore,
${{v}_{1}}=0$
Applying this assumption to equation 4, we have
${{v}_{2}}^{2}-{{v}_{1}}^{2}=2gh\Rightarrow {{v}_{2}}=\sqrt{2gh}$
Therefore, the mercury comes out of the hole with a speed of $\sqrt{2gh}$

Hence, the correct answer is option A.

Note:
The derivation we carried out in the above solution is nothing but a theorem called Torricelli’s theorem. Torricelli’s theorem states that the speed of a fluid$(v)$ through an opening at the bottom of a reservoir filled to a certain depth$(h)$ is the same as the speed of a freely falling object from a same height$(h)$, equal to the depth of the fluid. Mathematically, Torricelli’s theorem is represented by
$v=\sqrt{2gh}$
where
$v$ is the speed of the fluid through an opening
$h$ is the depth of the fluid inside the reservoir
This law also mentions that pressure increases with depth.