Question

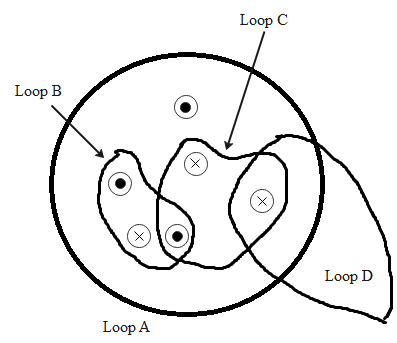
Consider six long wires with current coming into or out of the page, all with the same current. Rank the line integral of the magnetic field (from most positive to most negative) taken counter clockwise around each loop shown.

\[
  {\text{A}}{\text{. }}B > C > D > A \\
  {\text{B}}{\text{. }}B > C = D > A \\
  {\text{C}}{\text{. }}B > A > C = D \\
  {\text{D}}{\text{. }}C > B = D > A \\
\]

Answer 1

Hint: The value of the line integral of the magnetic field can be calculated by using the Ampere’s circuital law. The cross means that direction of magnetic field is inwards into the page and dot means that direction of the field is outwards of the page.

Formula used:

The expression for Ampere’s circuital law is given as

$\oint {\overrightarrow B .d\overrightarrow l } = {\mu _0}I{\text{ }}...\left( i \right)$
Here the left hand side represents the line integral of the magnetic field. I represent the current and ${\mu _0}$ is the permeability of the vacuum.

Detailed step by step solution:
We are given different loops of wires through which current is flowing. As we know that flow of current produces a magnetic field around the wire carrying the current.

The cross means that direction of magnetic field is inwards into the page while the dot means that direction of the field is outwards of the page.

We need to calculate the line integrals of the various loops. This can be done easily in terms of current by using the Ampere’s circuital law which is given by equation (i). It states that the line integral of the magnetic field is equal to the product of permeability and the current producing that magnetic field.

Now, let us use Ampere's circuital law to calculate the line integral of magnetic field for various loops.

Loop A: We have a total six fields; three coming out of the page and three are going into the page. This means we have three currents in anticlockwise direction while other three currents are in clockwise direction. Therefore the line integral of magnetic field is given as:
$\oint\limits_A {\overrightarrow B .d\overrightarrow l } = {\mu _0}\left( {I + I + I - I - I - I} \right) = 0$

Loop B: We have three fields; two coming out of the page and one going into the page. This means we have two currents in anticlockwise direction while one current is in clockwise direction. Therefore the line integral of magnetic field is given as:
$\oint\limits_B {\overrightarrow B .d\overrightarrow l } = {\mu _0}\left( {I + I - I} \right) = {\mu _0}I$

Loop C: We have three fields; one coming out of the page and two going into the page. This means we have one current in an anticlockwise direction while two currents are in clockwise direction. Therefore the line integral of magnetic field is given as:
$\oint\limits_C {\overrightarrow B .d\overrightarrow l } = {\mu _0}\left( {I - I - I} \right) = - {\mu _0}I$

Loop D: We have only one field going into the page. This means we have one current in its clockwise direction. Therefore the line integral of magnetic field is given as:
$\oint\limits_D {\overrightarrow B .d\overrightarrow l } = {\mu _0}\left( { - I} \right) = - {\mu _0}I$

Comparing all the line integrals we get,

$B > A > C = D$

Hence, the correct answer is option C.

Note: We can use the right hand thumb rule to calculate the direction of current due to the magnetic field and vice-versa. The anticlockwise current is taken as positive while the current flowing in clockwise direction is taken as negative in above equations.