Question

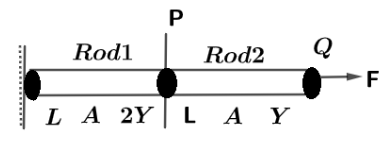
Consider an arrangement shown in the diagram which is a combination of two rods $(1)$ and $(2)$ .Their length, cross sectional area and Young modulus are shown in the diagram. If force $F$ is applied at the end of rod $(2)$ .then total elongation of the combined system is (P is the common end of rods $(1)$ and $(2)$ ).

A. $\dfrac{{3FL}}{{YA}}$
B. $\dfrac{{FL}}{{2YA}}$
C. $\dfrac{{3FL}}{{2YA}}$
D. $\dfrac{{FL}}{{YA}}$

Answer 1

Hint: In order to solve the above problem, we will find the elongation in each rods separately due to applied force and then add their elongation to get a net increase in length of the system.

Formula used:
Young modulus of a material is given as,
$Y = \dfrac{F}{A}\dfrac{{\Delta L}}{L}$
where $\Delta L$ denotes for elongation of a material and $A$ is the area of the cross section of given material.

Complete step by step answer:
Let us first find the $\Delta L$ for rod $(1)$ ,
We have, Force $ = F$
Young modulus $ = 2Y$
So, $\Delta {L_1} = \dfrac{{FL}}{{2AY}} \to (i)$ Using the Young modulus formula.
Similarly, we will find the elongation for rod $(2)$
Young modulus $ = Y$
So, $\Delta L$ for rod $(2)$ is given by,
$\Delta {L_2} = \dfrac{{FL}}{{AY}} \to (ii)$
Now, add both equations $(i)and(ii)$ we get,
$\text{Elongation} = \Delta {L_1} + \Delta {L_2}$
$\therefore \text{Elongation} = \dfrac{{3FL}}{{2AY}}$
So, the net elongation of the combined system is $\text{Elongation} = \dfrac{{3FL}}{{2AY}}$.

Hence, the correct option is C.

Note:Remember theoretically, Young modulus is defined as the ratio of stress (which is pressure acting on a material) to the strain (which is ratio of change in length of a body to its original length) and its SI unit is same as of Pressure $N{m^{ - 2}}$ . Also, in the given problem, Force was equally distributed along the line of two rods hence both rods were exerted by the same amount of force.