Question

Consider a triangular plot $ABC$ with sides $AB = 7m, BC = 5m$ and $CA = 6m$. A vertical lamp post at the midpoint $O$ of $AC$ substance an angle $30^\circ $ at $B.$ The height an ml of the lamp post is:
(A) $7\sqrt 3 $
(B) $\dfrac{2}{3}\sqrt {21} $
(C) $\dfrac{3}{2}\sqrt {21} $
(D) $2\sqrt {21} $

Answer 1

Hint: Use the trigonometric ratio of function:
(1) $\sin \theta = \dfrac{{{\text{Opposite side}}}}{{{\text{Hypotenuse}}}}$
(2) $\cos \theta = \dfrac{{{\text{Adjacent side}}}}{{{\text{Hypotenuse}}}}$
(3) $\tan \theta = \dfrac{{{\text{Opposite side}}}}{{{\text{Adjacent side}}}}$
Draw a triangle as per given information, name the points, make the distance as it gets easy to solve the problem.

Complete Step by Step Solution:
Given,
$AB = 7m$
$BC = 5m.$
$CA = 6m.$
To find: the height of the lamp-post.
Draw a triangle as per given information about the problem.

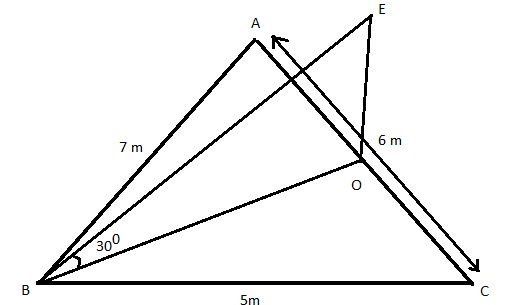
As per given information you have to draw a midpoint at side $AC$ and draw a line through $B$ at on $30^\circ $ angle. Means joint $(BO)$ and for finding the height of the lamp-post. Draw a line at $90^\circ $ straight. Mark that point as $'E'$ and joint $'BE'$
Here, you have to find $DE$ that is the height of the lamp-post.
So,
$BO = h\cot 30^\circ $
$BO = h\sqrt 3 $ (value of $\cot 30^\circ = \sqrt 3 )$
$A{B^2} + B{C^2} = 2\left( {B{O^2} + A{D^2}} \right)$
Put the value of the above sides.
${\left( 7 \right)^2} + {\left( 5 \right)^5} = 2\left[ {{{\left( {h\sqrt 3 } \right)}^2} + {3^2}} \right]$
$49 + 25 = 2\left( {3{h^2} + 9} \right)$
Here, ${\left( {h\sqrt 3 } \right)^2} = {h^2}\left( {\sqrt 3 \times \sqrt 3 } \right) = {h^2}3 = 3{h^2}$
$90^\circ = 2\left( {3{h^2} + 9} \right)$
above $'2'$ of right side will transfer to the left side and get division with $'74'$
Therefore,
$\dfrac{{74}}{2} = \left( {3{h^2} + 9} \right)$
$37 + 3{h^2} + 9$
Here, move constant terms to the one side and variable to another side.
$37 - 9 = 3{h^2}$
$28 = 3{h^2}$
Which can also be written as,
$3{h^2} = 28$
Here, transfer $'3'$ to the right side and convert into division.
${h^2} = \dfrac{{28}}{3}$
Here, the square of $'n'$ will transfer to the right side and get converted into square root.
$h = \sqrt {\dfrac{{28}}{3}} $
$ = \dfrac{{2\sqrt 7 }}{{\sqrt 3 }} \times \dfrac{{\sqrt 3 }}{{\sqrt 3 }}$
$h = \dfrac{{2\sqrt {21} }}{3}m$

Hence, the correct answer is option (B).

Additional information:
In mathematics the trigonometric function also called circular function, angle function or geometric function are real functions which relate an angle of a right angled triangle to a ratio of two side lengths. They are widely used in all sciences that are related to geometry, such as navigation, solid mechanics, celestial mechanics and many others. They are among the simplest periodic functions and as such are also widely used for studying periodic phenomena. Basis of trigonometry. If two right angles have equal acute angles they are similar so their lengths are proportional. Proportionality constants are written within $\sin \theta ,\cos \theta ,\tan \theta $ where $'\theta '$ is the common measure of five acute angles.

Note: Use the trigonometric identities, and function.
As you transfer one term to different sides therefore its sign will also change.
$' + '$ Addition will get converted into $' - '$ subtraction.
$' - '$ Subtraction will get converted into $' + '$ Addition.
$' \times '$ Multiplication will get converted into $' \div '$ division.
$' \div '$ division will get converted into $' \times '$ multiplication.