Question

Consider a triangle ABC and let a, b and c denote the lengths of the sides corresponding to vertices A, B and C respectively. Suppose a = 6, b = 10 and the area of the triangle is $15\sqrt 3 $. If $\angle $ACB is obtuse and if r denotes the radius of the incircle of the triangle, then ${r^2}$ is equal to

Answer 1

Hint: In this particular question use the concept that the area of the triangle is half times the multiplication of sine of angle and the corresponding sides of that angle and the radius of the incircle of the triangle is the ratio of the area of the triangle to the semi perimeter of the triangle, so use these concepts to reach the solution of the question.

Complete step-by-step answer:

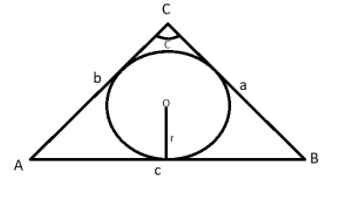
Given data:
In a triangle ABC and let a, b and c denote the lengths of the sides corresponding to vertices A, B and C respectively.
a = 6, b = 10 and the area of the triangle is $15\sqrt 3 $ square units.
Now as we know that the area of the triangle is half times the multiplication of sine of angle and the corresponding sides of that angle.
Let us consider the angle C, so the corresponding sides of angle C is a, and b, so the area of the triangle is,
$ \Rightarrow A = \dfrac{1}{2}ab\sin C$
Now substitute the values we have,
$ \Rightarrow 15\sqrt 3 = \dfrac{1}{2}\left( 6 \right)\left( {10} \right)\sin C$
$ \Rightarrow \sin C = \dfrac{{\sqrt 3 }}{2}$
Now it is given angle ACB is an obtuse angle.
As we know that an obtuse angle is always greater than 90 degrees.
$ \Rightarrow \sin C = \dfrac{{\sqrt 3 }}{2} = \sin {120^o}$
$ \Rightarrow C = {120^o}$
Now according to cosine law in a triangle we have,
$ \Rightarrow \cos C = \dfrac{{{a^2} + {b^2} - {c^2}}}{{2ab}}$
Now substitute the values in the above equation we have,
$ \Rightarrow \cos {120^o} = \dfrac{{{6^2} + {{10}^2} - {c^2}}}{{2\left( 6 \right)\left( {10} \right)}}$
Now simplify we have,
$ \Rightarrow - \dfrac{1}{2} = \dfrac{{36 + 100 - {c^2}}}{{120}}$,$\left[ {\because \cos {{120}^o} = - \dfrac{1}{2}} \right]$
$ \Rightarrow - 60 = 36 + 100 - {c^2}$
$ \Rightarrow {c^2} = 36 + 100 + 60 = 196 = {\left( {14} \right)^2}$
$ \Rightarrow c = 14$
Now as we know that the perimeter of any shape is the sum of all the side lengths.
So the perimeter of the triangle is the sum of all the lengths of the triangle.
So perimeter of the triangle is, P = a + b + c = 6 + 10 + 14 = 30
So the semi perimeter of the triangle is, $S = \dfrac{P}{2} = \dfrac{{30}}{2} = 15$
Now as we know that the radius of the incircle of the triangle is the ratio of the area of the triangle to the semi perimeter of the triangle.
So the radius of the incircle is, $r = \dfrac{A}{S} = \dfrac{{15\sqrt 3 }}{{15}} = \sqrt 3 $
So the value of ${r^2}$ is,
$ \Rightarrow {r^2} = {\left( {\sqrt 3 } \right)^2} = 3$
So this is the required answer.

Note: Whenever we face such types of questions the key concept we have to remember is that always recall the cosine law and the area of the triangle and the radius of the incircle which is all stated above, and always recall that the perimeter of any shape is the sum of all the side lengths. So the perimeter of the triangle is the sum of all the lengths of the triangle.