Question

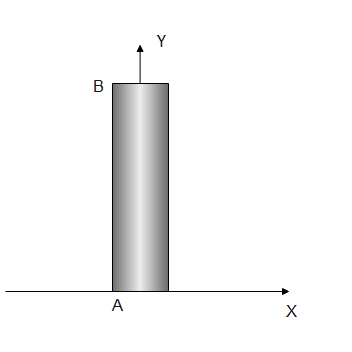
Consider a thin stick of length L. standing on one of its ends on a frictionless surface. It is slightly pushed at the other end of the rod. Then path of center of mass of the rod is

A. $\mathrm{x}=0$
B. $x^{2}+y^{2}=\dfrac{L^{2}}{4}$
C. $\mathrm{y}=0$
D. $\dfrac{\mathrm{x}^{2}}{\mathrm{L}^{2} /4}+\dfrac{\mathrm{y}^{2}}{\mathrm{L}^{2}}=1$

Answer 1

Hint: The center of mass of a spatial mass distribution is the particular point where the weighted relative location of the mass distributed amounts to zero. This is the point at which a force without an angular acceleration may be applied to induce a linear acceleration. The center of mass can be determined by taking the masses that you are trying to locate and multiplying the center of mass between them by their locations. You then add these together and divide them by the sum of all the masses of individuals.

Formula used:
$(\mathrm{x}-\mathrm{a})^{2}+(\mathrm{y}-\mathrm{b})^{2}=\mathrm{r}^{2}$

Complete step by step solution:
Since the stick is very small, the rod length is L From the figure, the stick is positioned at the center of the axis with one end $(\mathrm{x}=0, \mathrm{y}=0)$
Center of mass of the stick is at $\dfrac{\mathrm{L}}{2}$ distance from the edge. Center of mass of stick, follow circular path.
With radius $\mathrm{r}=\dfrac{\mathrm{L}}{2}$ center $(\mathrm{a}=0, \mathrm{b}=0)$
Apply the equation of the circle.
$\Rightarrow {{(\text{x}-\text{a})}^{2}}+{{(\text{y}-\text{b})}^{2}}={{\text{r}}^{2}}$
$\Rightarrow {{(\text{x}-0)}^{2}}+{{(\text{y}-0)}^{2}}={{\left( \dfrac{\text{L}}{2} \right)}^{2}}$
$\Rightarrow {{\text{x}}^{2}}+{{\text{y}}^{2}}=\dfrac{{{\text{L}}^{2}}}{4}$
\[\therefore \] Then path of center of mass of the rod is ${{\text{x}}^{2}}+{{\text{y}}^{2}}=\dfrac{{{\text{L}}^{2}}}{4}$

So, the correct answer is “Option B”.

Additional Information: It is the same as the center of mass in uniform gravity. It lies at the center of the specific body for regularly shaped bodies. Therefore, the center of gravity for a cylinder is at the midpoint of the cylinder 's axis. The mass center is a point of equilibrium for an object or a group of objects. For any single, two-, or three-dimensional object, the center of mass can be found, and so the units are meters (m) in each dimension.

Note: The center of mass can be determined by taking the masses that you are trying to locate and multiplying the center of mass between them by their locations. You then add these together and divide them by the sum of all the masses of individuals. At the center of the rod is the center of the mass of a uniform rod. So, for example, a uniform rod's center of mass