Question

Consider a cuboid of dimension 2*Roll, 4*roll and 6*Roll along the X, Y and Z axes, respectively. It is centered at the origin (O). The bottom face has vertices A, B, C and D. The top faces have vertices P, Q, R and S such that P is above A, and so on. Considering $\overset{\to }{\mathop{AP}}\,$as ${{\vec{F}}_{1}}$, determine the moment about O.

Answer 1

Hint: We are given a cuboid centered at the origin and also the dimensions of the cuboid along X, Y and Z axes. We know that moment about a point is the cross product of force and the distance from that point. Hence by finding the perpendicular distance from origin to the axes where force is considered we will get the solution.

Formula used: $M=\vec{F}\times r$

Complete step by step answer:
In the question we are given a cuboid of dimension $2\times 4\times 6$along the XY and Z axes respectively and centered at the origin.
We are given the bottom vertices of the cuboid as A, B, C and D and the top vertices as P, Q, R and S such that the vertex P is above A.
The figure given below shows us the given situation.

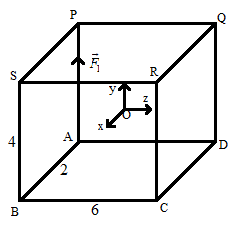
We are asked to find the moment about the origin (O) when $\overset{\to }{\mathop{AP}}\,={{\vec{F}}_{1}}$
We know that the equation for moment is given as the cross product of the force and distance, i.e.
$M=\vec{F}\times r$, where ‘$\vec{F}$’ is the force and ‘r’ is the radius.
$\Rightarrow M=\vec{F}r\sin \theta $
In this case the force is given as ${{\vec{F}}_{1}}$. Therefore we can write,
$\vec{F}={{\vec{F}}_{1}}$
And the perpendicular distance ‘r’ here is the perpendicular distance from the origin to the $\overset{\to }{\mathop{AP}}\,$ axis.
From the given figure, we can see that the distance from the origin to the $\overset{\to }{\mathop{AP}}\,$ axis is half of the distance from A to C, i.e.
$r=\dfrac{1}{2}AC$
Now, let us consider the bottom face as shown below.

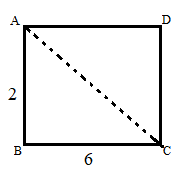
From this figure if we consider the right angled triangle ABC, by Pythagoras theorem we will get,
$A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}}$
Since, $AB=2$and $BC=6$, we can write
$\Rightarrow A{{C}^{2}}={{2}^{2}}+{{6}^{2}}$
$\Rightarrow A{{C}^{2}}=4+36$
$\Rightarrow A{{C}^{2}}=40$
$\Rightarrow AC=\sqrt{40}$
Therefore we get the perpendicular distance as,
$\Rightarrow r=\dfrac{1}{2}\times \sqrt{40}$
$\Rightarrow r=3.162$
Now we can calculate the moment as,
$\Rightarrow M={{\vec{F}}_{1}}\times 3.162\times \sin \theta $
Since ‘r’ is the perpendicular distance here, we have $\theta =90{}^\circ $. Thus the moment will become,
$\Rightarrow M={{\vec{F}}_{1}}\times 3.162\times \sin 90$
We know that $\sin 90=1$. Therefore,
$\Rightarrow M=3.162{{\vec{F}}_{1}}$

Thus the moment about O when $\overset{\to }{\mathop{AP}}\,={{\vec{F}}_{1}}$is $3.162{{\vec{F}}_{1}}$.

Note: Moment, also known as torque, is simply the product of force, the perpendicular distance from to the centre of gravity and also the sin of the angle between them. Moment is a static force whereas torque is a kinetic force. That is we use moments when there is no kind of rotation and torque is related with rotational motion.