Question

Consider a circular loop having current I and with central point O. the magnitude field at the central point is?

$\begin{align}
  & a)\dfrac{2{{\mu }_{\circ }}i}{3\pi R}acting\text{ }downward \\
 & b)\dfrac{5{{\mu }_{\circ }}i}{12R}acting\text{ }downward \\
 & c)\dfrac{6{{\mu }_{\circ }}i}{11R}acting\text{ }downward \\
 & d)\dfrac{5{{\mu }_{\circ }}i}{7R}acting\text{ }upward \\
\end{align}$

Answer 1

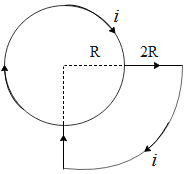
Hint: In the above figure we see a three fourth circle of radius R and one fourth circle of radius 3R. In the question we are asked to determine the magnetic field at point O. Hence we will use the expression for magnetic field due to a circular loop along its axis passing through the center in order to determine the field due to both the above loops at O.

Formula used:
$B=\dfrac{{{\mu }_{\circ }}i{{R}^{2}}}{2{{(x+{{R}^{2}})}^{3/2}}}$

Complete step by step answer:
In the above figure if we observe carefully, both the loops are placed with their centers at the same point i.e. at O. Let us say we have a circular loop with radius R and the current in the loop be i. Therefore the magnetic field (B)due to the loop along the axis passing through the center at a distance ‘x’ from the center is given by,
$B=\dfrac{{{\mu }_{\circ }}i{{R}^{2}}}{2{{(x+{{R}^{2}})}^{3/2}}}$
At the center of the circle we can imply that x=0. Therefore from above equation we get,
$\begin{align}
  & B=\dfrac{{{\mu }_{\circ }}i{{R}^{2}}}{2{{(x+{{R}^{2}})}^{3/2}}} \\
 & \Rightarrow B=\dfrac{{{\mu }_{\circ }}i{{R}^{2}}}{2{{(0+{{R}^{2}})}^{3/2}}}=\dfrac{{{\mu }_{\circ }}i{{R}^{2}}}{2{{R}^{3}}} \\
 & \Rightarrow B=\dfrac{{{\mu }_{\circ }}i}{2R} \\
\end{align}$
In the above figure the circle with radius R will have only 3/4 of its magnetic field at centre O. Hence from above equation we get the magnetic field H due to this loop as,
$H=\dfrac{3}{4}\dfrac{{{\mu }_{\circ }}i}{2R}=\dfrac{3{{\mu }_{\circ }}i}{8R}$
Similarly the magnetic field M due to the 1/4 sections of the circular loop with radius 3R is equal to,
$M=\dfrac{1}{4}\dfrac{{{\mu }_{\circ }}i}{2(3R)}=\dfrac{{{\mu }_{\circ }}i}{24R}$
Therefore the total magnetic field B at point O is equal to,
$\begin{align}
  & B=M+H \\
 & \Rightarrow B=\dfrac{{{\mu }_{\circ }}i}{24R}+\dfrac{3{{\mu }_{\circ }}i}{8R} \\
 & \Rightarrow B=\dfrac{{{\mu }_{\circ }}i}{24R}+\dfrac{9{{\mu }_{\circ }}i}{24R}=\dfrac{10{{\mu }_{\circ }}i}{24R} \\
 & \therefore B=\dfrac{5{{\mu }_{\circ }}i}{12R} \\
\end{align}$

So, the correct answer is “Option B”.

Note:
${{\mu }_{\circ }}$ is the permeability of free space. This factor basically depends on the medium in which the field is produced. It is also to be noted that we have added the magnetic field as they have the same direction. In order to determine the direction of the field, curl your right hand in the direction of the current in the coil, then the thumb will indicate the direction of the field.