Question

Concrete can be purchased by the cubic yard. How much will it cost to pour a slab $11$ feet by $11$ feet by $3$ inches for a patio if the concrete costs $\$63.00$ per cubic yard?

Answer 1

Hint: For this problem we need to calculate the cost of the concrete which is used in the construction of a slab with the given dimensions. We can observe that the given dimensions of the slab are not in the same unit. So, we will convert all the given dimensions into a single unit by using the known relations between the units. After that we will calculate the volume of the concrete needed to construct a cuboid slab by using the formula volume of the cuboid as $l\times b\times h$. Now we will get the volume in cubic feet. But the cost of concrete is measured in cubic yards. So here also we will use unit conversion to calculate the volume of concrete required for the slab in the cubic yard. Now we can easily calculate the required value by multiplying the given cost with the calculated
volume in cubic yards.

Complete step by step solution:
Given that, Dimensions of the slab are $11$ feet by $11$ feet by $3$ inches.

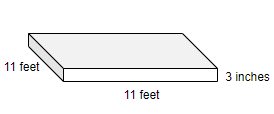
Here we have the height or depth of slab in inches. We know that $12$ inches $=$ $1$ feet. From this we can write
$\begin{align}
  & 3\text{ inches}=\dfrac{3}{12}\text{ feet} \\
 & \Rightarrow 3\text{ inches}=\dfrac{1}{4}\text{ feet} \\
\end{align}$
Now the volume of the slab is given by
$\begin{align}
  & \Rightarrow v=11\times 11\times \dfrac{1}{4} \\
 & \Rightarrow v=\dfrac{121}{4}\text{ cubic feet} \\
\end{align}$
Here we have the volume of concrete in cubic feet. We know that $1\text{ cubic feet}=\dfrac{1}{27}\text{ cubic yards}$. From this relation we can write the volume of concrete as
$\begin{align}
  & \Rightarrow v=\dfrac{121}{4}\times \dfrac{1}{27}\text{ cubic yard} \\
 & \Rightarrow v=\dfrac{121}{108}\text{ cubic yard} \\
\end{align}$
In this problem we have the cost of the concrete as $\$63.00$ per cubic yard. Hence the cost of the total concrete required is given by
$\begin{align}
  & \Rightarrow c=\dfrac{121}{108}\times \$63.00\\&\Rightarrow c=\$70.62\\\end{align}$
Hence the cost of the slab is $\$70.62$.

Note:
In this problem we don’t have the detailed explanation on the dimensions of the slab, then have given orally as $11$ feet by $11$ feet by $3$ inches. So, we need to assume that the given slab is in cuboidal shape and calculate the volume of the slab.