Question

How many complex roots does \[6{{x}^{5}}+{{x}^{4}}-3=0\] have?

Answer 1

Hint: These types of problems are pretty simple to solve and they are easy to understand. There are of course many methods to solve this particular question, but the simplest of them is just to plot the above mentioned graph of the equation \[6{{x}^{5}}+{{x}^{4}}-3=0\] . Now by looking at the nature of the graph as well as the roots, we can very easily predict the number of complex roots as well as imaginary roots of the equation.

Complete step by step answer:
Now starting off with the given problem equation solution, we plot the graph for \[6{{x}^{5}}+{{x}^{4}}-3=0\] . Now the following rules should be obeyed in determining the roots of the equation. They are,
1. If the graph cuts the x-axis at different points, then these points are the real roots of the equation.
2. Since the given problem is a polynomial of degree \[5\] , thus there should always be \[5\] roots for this equation. Some of them may be imaginary whereas some of them are real. Complex roots, if they occur, always occur in pairs.
The graph of the given equation is thus,

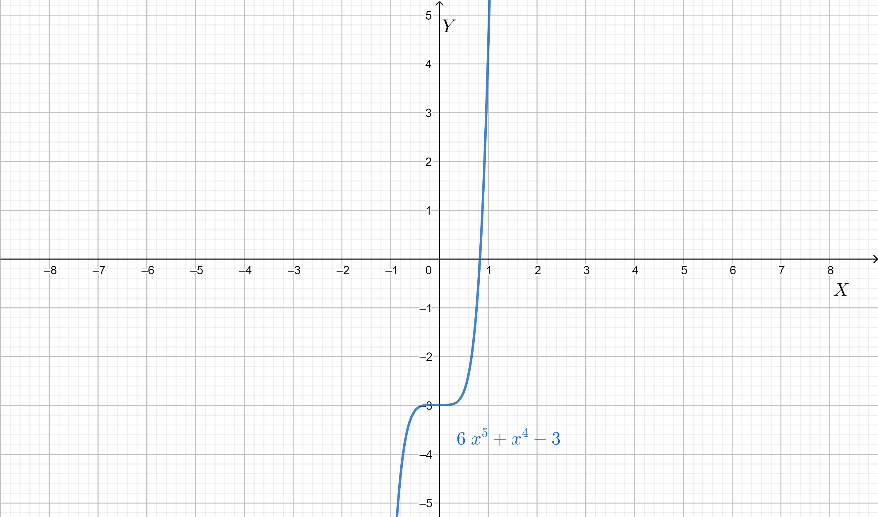
From the above graph we can conclude that, there is only one real root of this equation, which is the point where the graph cuts the x-axis. Therefore we can clearly estimate that there are exactly \[4\] imaginary roots because the total number of roots has to be equal to the degree \[5\] .

Note: In these types of questions the most important thing is to plot the required graph of the equation which can be easily done by a little knowledge of graph theory. This plot of the graph can easily be done by finding the first derivative, thereby using the critical points to find the point of maxima and minima. We can further do the second derivative to find the curvature of the graph as well.