Question

Complete the sequence:
\[\text{17},\text{ 15},\text{ 26},\text{ 22},\text{ 35},\text{ 29},\text{ }\underline{?},\text{ }\underline{?}\]

Answer 1

Hint: The above question is a somewhat reasoning type question, which can be done by various tricks and methods. The approach is simple and catchy. Compare each next term with the previous term and observe what kind of relationship we have. After observing we simply apply these relations to the next upcoming terms. Try finding the difference between the alternate set of terms like for 17, 15 then 26, then for 35, 29, and then proceed further.

Complete step-by-step solution:
Let’s move ahead to our question, complete the sequence \[\text{17},\text{ 15},\text{ 26},\text{ 22},\text{ 35},\text{ 29},\text{ }\underline{?},\text{ }\underline{?}\]

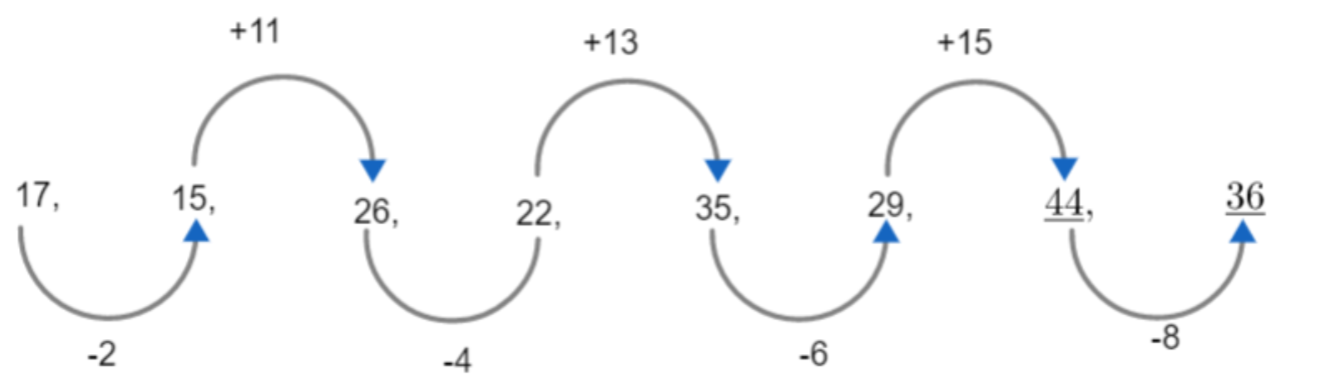
The above figure, uses two operations:
\[\begin{align}
  & \text{First:} \\
 & \text{17}-\text{2}=\text{15} \\
 & \text{26}-\text{4}=\text{22} \\
 & \text{35}-\text{6}=\text{29} \\
 & \text{44}-\text{8}=\text{36} \\
\end{align}\]
\[\begin{align}
  & \text{Second:} \\
 & \text{15}+\text{11}=\text{26} \\
 & \text{22}+\text{13}=\text{35} \\
 & \text{29}+\text{15}=\text{44} \\
\end{align}\]
In first operation, alternate terms are subtracted by increasing even numbers i.e. 2, 4, 6, 8 . . . . .
In second operation, second term is increased by 11, then alternate terms are increased by \[\begin{matrix}
   11+2, \\
   \begin{align}
  & \downarrow \\
 & \left( 13 \right) \\
\end{align} \\
\end{matrix}\begin{matrix}
   11+4, \\
   \downarrow \\
   \left( 15 \right) \\
\end{matrix}\begin{matrix}
   11+6 \\
   \downarrow \\
   \left( 17 \right) \\
\end{matrix}\text{ }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{.}\]
In this way, we get our next two terms as 44 and 36.

Note: The chances of mistakes are less once we get the logic. By the way, this question can also be done with one other method.
Given series: \[\text{17},\text{ 15},\text{ 26},\text{ 22},\text{ 35},\text{ 29},\text{ }\underline{?},\text{ }\underline{?}\]
We can write above series as the combination of two arithmetic series, i.e.
\[\text{17},\text{ 15},\text{ }\left( \text{17}+\text{9} \right),\text{ }\left( \text{15}+\text{7} \right),\text{ }\left( \text{17}+\text{9}+\text{9} \right),\text{ }\left( \text{15}+\text{7}+\text{7} \right)\text{ }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{.}\]
\[\begin{align}
  & \text{First AP}:\text{ 17},\text{ }\left( \text{17}+\text{9} \right),\text{ }\left( \text{17}+\text{9}+\text{9} \right),\text{ }\left( \text{17}+\text{9}+\text{9}+\text{9} \right)\text{ }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. } \\
 & \text{Second AP}:\text{ 15},\text{ }\left( \text{15}+\text{7} \right),\text{ }\left( \text{15}+\text{7}+\text{7} \right),\text{ }\left( \text{15}+\text{7}+\text{7}+\text{7} \right)\text{ }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{.} \\
\end{align}\]
Now, by calculating above two series, we get:
\[\begin{align}
  & \Rightarrow \text{17},\text{15},\left( \text{17}+\text{9} \right),\left( \text{15}+\text{7} \right),\left( \text{17}+\text{9}+\text{9} \right),\left( \text{15}+\text{7}+\text{7} \right),\left( \text{17}+\text{9}+\text{9}+\text{9} \right),\left( \text{15}+\text{7}+\text{7}+\text{7} \right)\text{ }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. } \\
 & \Rightarrow \text{17},\text{ 15},\text{ 26},\text{ 22},\text{ 35},\text{ 29},\text{ 44},\text{ 36 }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{.} \\
\end{align}\]
Hence, we get 44 and 36 as answers.