
Complete the given table and draw a graph for each:
\[x\] \[1\] \[2\] \[4\] \[6\] \[y = x - 1\] \[0\]
| \[x\] | \[1\] | \[2\] | \[4\] | \[6\] |
| \[y = x - 1\] | \[0\] |
Answer
571.8k+ views
Hint: We will calculate the values of one variable by using the second variable and the relation between them. After that by using the coordinates of \[x\] and \[y\], we will draw the graphs.
Complete step-by-step solution:
Step 1: For calculating the value of \[y\] we will use the equation \[y = x - 1\] for all values \[x\] as shown below:
If \[x = 1\] then by substituting this value in the equation,\[y = x - 1\] we get:
\[ \Rightarrow y = 1 - 1\]
By doing subtraction into the RHS side of the above equation we get:
\[ \Rightarrow y = 0\] ……………….. (1)
If \[x = 2\] then by substituting this value in the equation,
\[y = x - 1\] we get:
\[ \Rightarrow y = 2 - 1\]
By doing subtraction into the RHS side of the above equation we get:
\[ \Rightarrow y = 1\] …………………… (2)
If \[x = 4\] then by substituting this value in the equation,
\[y = x - 1\] we get:
\[ \Rightarrow y = 4 - 1\]
By doing subtraction into the RHS side of the above equation we get:
\[ \Rightarrow y = 3\] …………………….. (3)
If \[x = 6\] then by substituting this value in the equation,
\[y = x - 1\] we get:
\[ \Rightarrow y = 6 - 1\]
By doing subtraction into the RHS side of the above equation we get:
\[ \Rightarrow y = 5\] ………………………. (4)
Step 2: From the equation (1), (2), (3), and (4) we got the values of \[y\] co-ordinate w.r.t \[x\]. So, the points will become as below:
\[ \Rightarrow \left( {1,0} \right)\],
\[\left( {2,1} \right)\],\[\left( {4,3} \right)\] and \[\left( {6,5} \right)\]
Step 3: The graphs of the respective points
\[\left( {1,0} \right)\], \[\left( {2,1} \right)\],\[\left( {4,3} \right)\] and \[\left( {6,5} \right)\] are shown below:
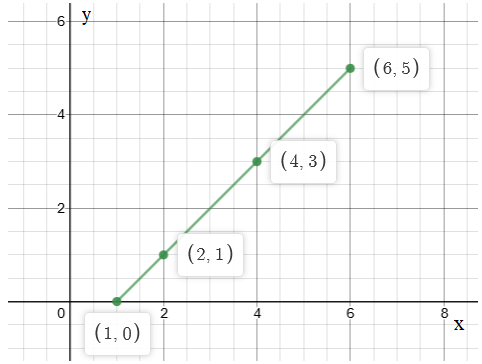
The final table is as below:
Note: Students generally make mistakes in the axis of the graphs. You should remember that the horizontal line is known as the \[x\]-axis of the graph and the vertical line is the \[y\] axis.
Complete step-by-step solution:
Step 1: For calculating the value of \[y\] we will use the equation \[y = x - 1\] for all values \[x\] as shown below:
If \[x = 1\] then by substituting this value in the equation,\[y = x - 1\] we get:
\[ \Rightarrow y = 1 - 1\]
By doing subtraction into the RHS side of the above equation we get:
\[ \Rightarrow y = 0\] ……………….. (1)
If \[x = 2\] then by substituting this value in the equation,
\[y = x - 1\] we get:
\[ \Rightarrow y = 2 - 1\]
By doing subtraction into the RHS side of the above equation we get:
\[ \Rightarrow y = 1\] …………………… (2)
If \[x = 4\] then by substituting this value in the equation,
\[y = x - 1\] we get:
\[ \Rightarrow y = 4 - 1\]
By doing subtraction into the RHS side of the above equation we get:
\[ \Rightarrow y = 3\] …………………….. (3)
If \[x = 6\] then by substituting this value in the equation,
\[y = x - 1\] we get:
\[ \Rightarrow y = 6 - 1\]
By doing subtraction into the RHS side of the above equation we get:
\[ \Rightarrow y = 5\] ………………………. (4)
Step 2: From the equation (1), (2), (3), and (4) we got the values of \[y\] co-ordinate w.r.t \[x\]. So, the points will become as below:
\[ \Rightarrow \left( {1,0} \right)\],
\[\left( {2,1} \right)\],\[\left( {4,3} \right)\] and \[\left( {6,5} \right)\]
Step 3: The graphs of the respective points
\[\left( {1,0} \right)\], \[\left( {2,1} \right)\],\[\left( {4,3} \right)\] and \[\left( {6,5} \right)\] are shown below:

The final table is as below:
| \[x\] | \[1\] | \[2\] | \[4\] | \[6\] |
| \[y = x - 1\] | \[0\] | \[1\] | \[3\] | \[5\] |
Note: Students generally make mistakes in the axis of the graphs. You should remember that the horizontal line is known as the \[x\]-axis of the graph and the vertical line is the \[y\] axis.
Recently Updated Pages
Master Class 8 Social Science: Engaging Questions & Answers for Success

Master Class 8 English: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Master Class 8 Maths: Engaging Questions & Answers for Success

Master Class 8 Science: Engaging Questions & Answers for Success

Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Trending doubts
What is BLO What is the full form of BLO class 8 social science CBSE

Citizens of India can vote at the age of A 18 years class 8 social science CBSE

Full form of STD, ISD and PCO

Advantages and disadvantages of science

Right to vote is a AFundamental Right BFundamental class 8 social science CBSE

What are the 12 elements of nature class 8 chemistry CBSE





