
Complete the following table to draw the graph of $ y = 2x + 1 $
X 2 -2 ............ ........... Y ................... ............... -5 3
| X | 2 | -2 | ............ | ........... |
| Y | ................... | ............... | -5 | 3 |
Answer
564.6k+ views
Hint: Here in this question first we need to find the value of X and Y by using the graph equation. Substituting the known values to the equation we can find the value unknown of the equation. Hence we can plot the graph by using the values.
Complete step-by-step answer:
In the question they have given a table which contains the values of X and Y. The equation of a graph is given as $ y = 2x + 1 $ .
Now we consider the value of X and we substitute in the equation of graph $ y = 2x + 1 $ , hence we can find the value of Y
Consider the equation of graph $ y = 2x + 1 $ ------ (1)
Substitute the value of X as 2 in equation (1). So we have
$
\Rightarrow y = 2(2) + 1 \\
\Rightarrow y = 4 + 1 \\
\Rightarrow y = 5 \;
$
When X is 2 the value of Y is 5
Substitute the value of X as -2 in equation (1). So we have
$
\Rightarrow y = 2( - 2) + 1 \\
\Rightarrow y = - 4 + 1 \\
\Rightarrow y = - 3 \;
$
When X is -2 the value of Y is -3
Now in the question they have given the value of Y. Therefore
Substitute the value of Y as -5 in equation (1). So we have
$
\Rightarrow - 5 = 2x + 1 \\
\Rightarrow - 5 - 1 = 2x \\
\Rightarrow - 6 = 2x \\
\Rightarrow x = \dfrac{{ - 6}}{2} \\
\Rightarrow x = - 3 \;
$
When Y is -5 the value of X is -3
Substitute the value of Y as 3 in equation (1). So we have
$
\Rightarrow 3 = 2x + 1 \\
\Rightarrow 3 - 1 = 2x \\
\Rightarrow 2 = 2x \\
\Rightarrow x = \dfrac{2}{2} \\
\Rightarrow x = 1 \;
$
When Y is 3 the value of X is 1.
Therefore we have table as
Considering these points we can plot the graph. The graph is shown below.
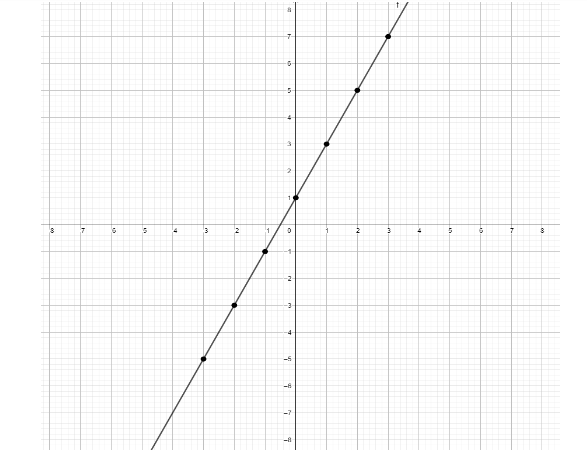
Note: The graph is plotted against the two axes namely X-axis and Y-axis. If we know the value of the one we can find the other by using the equation of the graph. This graph is two dimensional because they have mentioned only two axes.
Complete step-by-step answer:
In the question they have given a table which contains the values of X and Y. The equation of a graph is given as $ y = 2x + 1 $ .
Now we consider the value of X and we substitute in the equation of graph $ y = 2x + 1 $ , hence we can find the value of Y
Consider the equation of graph $ y = 2x + 1 $ ------ (1)
Substitute the value of X as 2 in equation (1). So we have
$
\Rightarrow y = 2(2) + 1 \\
\Rightarrow y = 4 + 1 \\
\Rightarrow y = 5 \;
$
When X is 2 the value of Y is 5
Substitute the value of X as -2 in equation (1). So we have
$
\Rightarrow y = 2( - 2) + 1 \\
\Rightarrow y = - 4 + 1 \\
\Rightarrow y = - 3 \;
$
When X is -2 the value of Y is -3
Now in the question they have given the value of Y. Therefore
Substitute the value of Y as -5 in equation (1). So we have
$
\Rightarrow - 5 = 2x + 1 \\
\Rightarrow - 5 - 1 = 2x \\
\Rightarrow - 6 = 2x \\
\Rightarrow x = \dfrac{{ - 6}}{2} \\
\Rightarrow x = - 3 \;
$
When Y is -5 the value of X is -3
Substitute the value of Y as 3 in equation (1). So we have
$
\Rightarrow 3 = 2x + 1 \\
\Rightarrow 3 - 1 = 2x \\
\Rightarrow 2 = 2x \\
\Rightarrow x = \dfrac{2}{2} \\
\Rightarrow x = 1 \;
$
When Y is 3 the value of X is 1.
Therefore we have table as
| X | 2 | -2 | -3 | 1 |
| Y | 5 | -3 | -5 | 3 |
Considering these points we can plot the graph. The graph is shown below.

Note: The graph is plotted against the two axes namely X-axis and Y-axis. If we know the value of the one we can find the other by using the equation of the graph. This graph is two dimensional because they have mentioned only two axes.
Recently Updated Pages
Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Physics: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Trending doubts
What is BLO What is the full form of BLO class 8 social science CBSE

Citizens of India can vote at the age of A 18 years class 8 social science CBSE

Full form of STD, ISD and PCO

Convert 40circ C to Fahrenheit A 104circ F B 107circ class 8 maths CBSE

Advantages and disadvantages of science

Right to vote is a AFundamental Right BFundamental class 8 social science CBSE




