Question

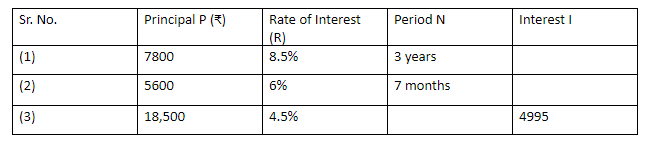
Complete the following table.

Answer 1

Hint: In this question we are given three cases involving computation of Simple Interest. So we will use the formula for Simple Interest to find the missing values.
The formula for simple interest is given as:
$SI = \dfrac{{P \times R \times t}}{{100}}$, with P as principal , r as rate of interest and t is the time period.

Complete step by step solution: Now for Case (1), it is given,
$ P = 7800 \\
  R = 8.5\% \\
  t = 3years \\ $
So, $SI = \dfrac{{P \times R \times t}}{{100}}$
Now, putting the values of P, R and t in the formula for SI we will get the SI as:
$ SI = \dfrac{{7800 \times 8.5 \times 3}}{{100}} \\
   = \dfrac{{7800 \times 85 \times 3}}{{1000}} \\
   = 1989 \\ $
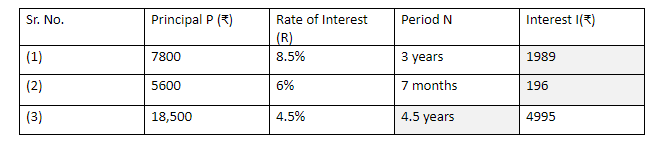
So, the interest is ₹1989.
Now, for the next case, that is (2), it is given:
$ P = 5600 \\
  R = 6\% \\
  t = 7months \\ $
Now, here the time is 7months so we have to consider it as a fraction of a year, that is 12 months for calculating the interest.
So, $SI = \dfrac{{P \times R \times t}}{{100}}$
Now, putting the values of P, R and t in the formula for SI we will get the SI as:
$ SI = \dfrac{{5600 \times 6 \times 7}}{{100 \times 12}} \\
   = 28 \times 7 \\
   = 196 \\ $
So, the interest is ₹196.
Now, for the next case, that is (3), it is given:
$ P = 18500 \\
  R = 4.5\% \\
  t = ? \\
  SI = 4995 \\ $
Now, here everything including the interest is given except for the time. So we have to find the etime to fill up the blank. Now interest is given as:
So, $SI = \dfrac{{P \times R \times t}}{{100}}$
Now, putting the values of P, R and t in the formula for SI we will get the SI as:
$ SI = \dfrac{{18500 \times 4.5 \times N}}{{100}} \\
  4995 = \dfrac{{18500 \times 45 \times N}}{{1000}} \\
  4995 = \dfrac{{185 \times 9 \times N}}{2} \\
  N = \dfrac{{4995 \times 2}}{{185 \times 9}} \\
  N = \dfrac{{27 \times 2}}{9} \\
  N = 54months \\
  N = \dfrac{{54}}{{12}}years \\
  N = \dfrac{{18}}{4} \\
  N = 4\dfrac{1}{2}years \\
  N = 4.5years \\ $
So, the missing value of time is 4.5 years.
So the table will now become:
 

Note: In this question, or the second case, the time has to be taken as a fraction of 1 year since simple interest is always calculated with the time in years. Whenever the time for Simple interest is given in months, it is to be written as a fraction of a year of 12 months. Also, interest and simple interest mean the same thing unless mentioned specifically at Compound interest.