Question

Complete the following statement: Among two congruent angles, one has a measure of ${{70}^{\circ }}$; the measure of the other angle is _________. \[\]

Answer 1

Hint: We recall the definition of angle, the measure of an angle, and the congruence condition of figures on a plane. We use the fact that two angles are congruent if and only if their measures are equal and find the measurement of the other angles.

Complete step-by-step solution:
We know that angle is a figure formed in the plane by two rays having a common point. The common point is called the vertex of the angle and the4 rays are called sides. If $\overrightarrow{OA},\overrightarrow{OB}$ be two rays that form an angle with vertex O then the angle is denoted $\angle AOB$ whose rough figure is drawn below.\[\]

We know that the measure of an angle is the amount of rotation from one ray to another. It is measured as the ratio of the length of a circular arc centered at the vertex and bounded by two rays. The measure of angle $\angle AOB$ is denoted by $m\angle AOB$ or simply $\angle AOB$.\[\]
We also know that two figures on a plane are congruent when they have the same shape and size. If the figures are defined by parameters then they are congruent when the parameters are equal. For example, the parameter of the line segment is ‘length’. Two line segments are going to be congruent if their lengths are equal. \[\]
Similarly, we see that the parameter for an angle is its measure and hence two angles are going to be congruent when their measures will be equal. We are given the question that among two congruent angles, one has a measure of${{70}^{\circ }}$. Let that angle is $\angle AOB$ and its congruent angle is $\angle PQR$. So we have,
\[\angle AOB={{70}^{\circ }}\]
If $\angle AOB$ and $\angle PQR$ are congruent then we have,
\[\angle AOB=\angle PQR\]
So we have the measure of the other angle as
\[\angle PQR={{70}^{\circ }}\]
 

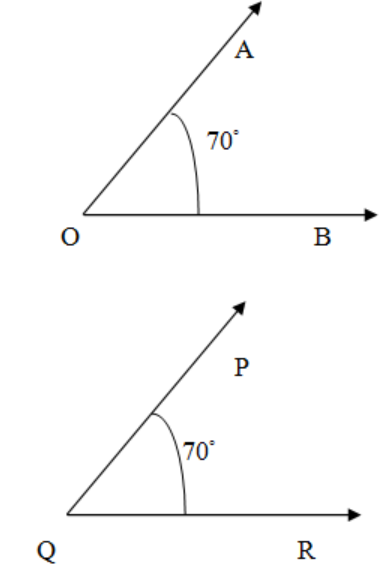
So we need to fill ${{70}^{\circ }}$ in the blank to complete the sentence. \[\]

Note: We note that when the measure of the angle measures the smaller angle (acute or obtuse) between two rays, not the reflex angle. The units of measure of angle are degree and radian. The examples of angles, which are always congruent are vertically opposite angles, alternate angles, interior angles in an equilateral triangle, etc.