Question

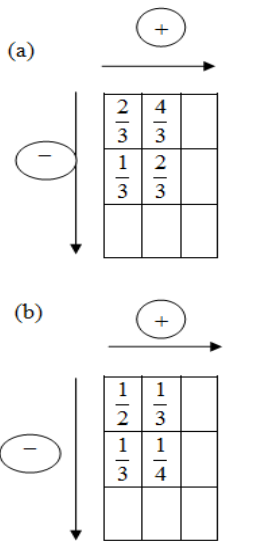
Complete the addition and subtraction box.\[\]

Answer 1

Hint: We see from the given question we have to add when we move towards the right and subtract when we move towards the bottom. We add the entries in the first two-row and write the respective sums in the empty squares of the third column. We subtract the entries of the second column from the first column respectively and write them in the empty squares of the third row. We can fill the empty square at the corner in the third-row third column by adding the entries at its left that or with the difference of entries right above. \[\]

Complete step-by-step solution:
Let us observe the addition subtraction box in the part (a) of the question.

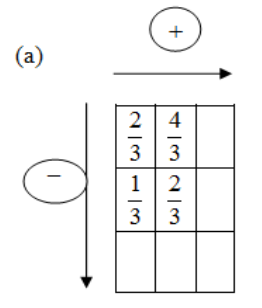
We see that in the box is a $3\times 3$ square. So there are 9 squares with two squares in each of the first rows and the second row is filled. The numbers in the first row are $\dfrac{2}{3},\dfrac{4}{3}$ and the numbers in the second row are $\dfrac{1}{3},\dfrac{2}{3}$. \[\]
The arithmetic operation that is denoted above the square is an addition directed towards the right. So we add $\dfrac{2}{3},\dfrac{4}{3}$, and write the result in an empty square present in the first-row third column. We have
\[\dfrac{2}{3}+\dfrac{4}{3}=\dfrac{6}{3}=2\]
Similarly we add $\dfrac{1}{3},\dfrac{2}{3}$, and write the sum in empty square present in the result in the second-row third column.
\[\dfrac{1}{3}+\dfrac{2}{3}=\dfrac{3}{3}=1\]
The arithmetic operation that is denoted left of the square is the addition directed downward. We subtract $\dfrac{1}{3}$ from $\dfrac{2}{3}$ and write the result in result in empty square present in the third-row first column. We have
\[\dfrac{2}{3}-\dfrac{1}{3}=\dfrac{1}{3}\]
Similarly, we add $\dfrac{1}{3}$ from $\dfrac{2}{3}$ and write the difference in empty square present in the result in the third-row second column. We have,
\[\dfrac{4}{3}-\dfrac{2}{3}=\dfrac{2}{3}\]
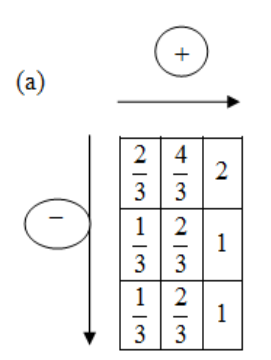
We can fill the empty square at the corner in the third-row third column by adding the entries at its left that or with the difference of entries right above. So we have
\[\begin{align}
  & \dfrac{1}{3}+\dfrac{2}{3}=1 \\
 & 2-1=1 \\
\end{align}\]
So we have the same result and its value is 1. So the filled up box is.

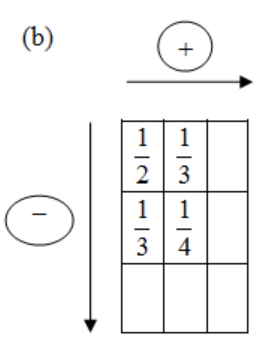
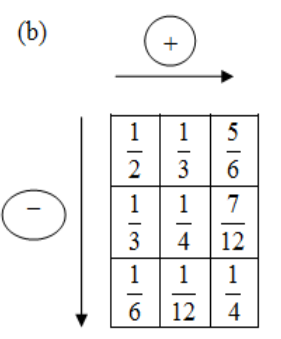
Similarly, we solve for the box in part(b).

We add the entries in the first two row and write the respective sums in the empty squares of third column.
\[\begin{align}
  & \dfrac{1}{2}+\dfrac{1}{3}=\dfrac{5}{6} \\
 & \dfrac{1}{3}+\dfrac{1}{4}=\dfrac{7}{12} \\
\end{align}\]
We subtract the entries of second column from the first column respectively and write them in the empty squares of third row. We have,
\[\begin{align}
  & \dfrac{1}{2}-\dfrac{1}{3}=\dfrac{1}{6} \\
 & \dfrac{1}{3}-\dfrac{1}{4}=\dfrac{1}{12} \\
\end{align}\]
We can fill the empty square at the corner in third row third column by adding the entries at its left that or with difference of entries right above. So we have
\[\begin{align}
  & \dfrac{1}{6}+\dfrac{1}{12}=\dfrac{3}{12}=\dfrac{1}{4} \\
 & \dfrac{5}{6}-\dfrac{7}{12}=\dfrac{3}{12}=\dfrac{1}{4} \\
\end{align}\]
 So the filled up square is

Note: We need to be careful of the signs of operations while we are filling the box. We also note that the addition of fractions always must be done by finding the least multiple (LCM) of denominators first. If the operations would not have given in the question then we would have to find the operation with trial and error and then fill up the squares.