Question

What is the complementary angle to $ 42^\circ $ ?

Answer 1

Hint: We are supposed to find the complementary angle of $ 42^\circ $ . Two angles are said to be complementary when their sum is equal to $ 90^\circ $ . Suppose the complementary of $ 42^\circ $ is x. Therefore, x plus 42 must be equal to 90. Hence, we get our equation $ x + 42^\circ = 90^\circ $ . Solving this equation, we will get our answer.

Complete step-by-step answer:
In this question, we are supposed to find a complementary angle of $ 42^\circ $ .
Let the complementary angle to $ 42^\circ $ be x.
First of all, let us understand what complementary angles are.
Two angles are said to be complementary, if their sum equals to $ 90^\circ $ and if their sum equals to $ 180^\circ $ , they are called supplementary angles.

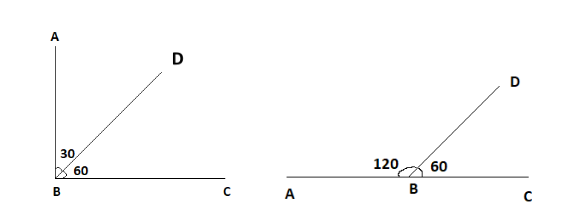
For example: Suppose we are given two angles $ 30^\circ $ and $ 60^\circ $ , then they sum up to $ 30^\circ + 60^\circ = 90^\circ $ .Hence they are complementary angles to each other.
Suppose we are given two angles $ 120^\circ $ and $ 60^\circ $ , then they sum up to $ 120^\circ + 60^\circ = 180^\circ $ . Hence, they are supplementary angles to each other.
Now, we have to find the complementary angle of $ 42^\circ $ .
Therefore, x plus 42 must be equal to 90.
 $ \Rightarrow x + 42^\circ = 90^\circ $
Make x the subject of the equation and simplify the equation, we get
 $
   \Rightarrow x = 90^\circ - 42^\circ \\
   \Rightarrow x = 48^\circ \;
  $
Hence, the complementary angle to $ 42^\circ $ is $ 48^\circ $ .
So, the correct answer is “ $ 48^\circ $ ”.

Note: We can cross check our answer by adding 42 to 48 and as they are complementary angles the answer should be 90.
\[ \Rightarrow 42^\circ + 48^\circ = 90^\circ \]
Hence, our answer is correct.