
${\text{C}}{{\text{N}}^ - }$and ${{\text{N}}_{\text{2}}}$ are isoelectronic. But in contrast to ${\text{C}}{{\text{N}}^ - }$,${{\text{N}}_{\text{2}}}$is chemically inert because of:
A. Smaller N-N bond energy
B. Larger N-N bond energy
C. Low ionization energy
D. None of these
Answer
559.2k+ views
Hint: The chemical inertness means the ${{\text{N}}_{\text{2}}}$is very stable. We have to determine the reason for the stability of ${{\text{N}}_{\text{2}}}$. The chemical inertness depends upon a lot of factors such as size, bond energy, electronic configuration, polarity, bond order, etc. we will draw the structure of the given molecules and will write electronic configurations to determine the factor responsible for the stability of the ${{\text{N}}_{\text{2}}}$.
Complete step-by-step answer:
The molecular electronic configuration of ${\text{C}}{{\text{N}}^ - }$and ${{\text{N}}_{\text{2}}}$are as follows:
\[{{\text{N}}_{\text{2}}}\,{\text{ = }}{\left( {{{1s\sigma}}} \right)^{\text{2}}}{\left( {{\text{1s}}{{{\sigma}}^{\text{*}}}} \right)^{\text{2}}}{\left( {{{2s\sigma}}} \right)^{\text{2}}}{\left( {{\text{2s}}{{{\sigma}}^{\text{*}}}} \right)^{\text{2}}}{\left( {{\text{2}}{{\text{p}}_{\text{x}}}{{\pi}} \approx {\text{2}}{{\text{p}}_{\text{y}}}{{\pi}}} \right)^4}{\left( {{\text{2}}{{\text{p}}_{\text{Z}}}{{\sigma}}} \right)^2}\left( {{\text{2}}{{\text{p}}_{\text{x}}}{{{\pi}}^{\text{*}}} \approx {\text{2}}{{\text{p}}_{\text{y}}}{{{\pi}}^{\text{*}}}} \right)\left( {{\text{2}}{{\text{p}}_{\text{Z}}}{{{\sigma}}^{\text{*}}}} \right)\]
\[{\text{C}}{{\text{N}}^ - }\,{\text{ = }}{\left( {{{1s\sigma}}} \right)^{\text{2}}}{\left( {{\text{1s}}{{{\sigma}}^{\text{*}}}} \right)^{\text{2}}}{\left( {{{2s\sigma}}} \right)^{\text{2}}}{\left( {{\text{2s}}{{{\sigma}}^{\text{*}}}} \right)^{\text{2}}}{\left( {{\text{2}}{{\text{p}}_{\text{x}}}{{\pi}} \approx {\text{2}}{{\text{p}}_{\text{y}}}{{\pi}}} \right)^4}{\left( {{\text{2}}{{\text{p}}_{\text{Z}}}{{\sigma}}} \right)^2}\left( {{\text{2}}{{\text{p}}_{\text{x}}}{{{\pi}}^{\text{*}}} \approx {\text{2}}{{\text{p}}_{\text{y}}}{{{\pi}}^{\text{*}}}} \right)\left( {{\text{2}}{{\text{p}}_{\text{Z}}}{{{\sigma}}^{\text{*}}}} \right)\]
The formula to determine the bond order is as follows:
Bonding electron – Anti bonding electrons / $2$
Bond order of${{\text{N}}_{\text{2}}}$,
${{\text{N}}_{\text{2}}}\, = \,\dfrac{{10 - 4}}{2}$
${{\text{N}}_{\text{2}}}\, = \,3$
Bond order of${\text{C}}{{\text{N}}^ - }$,
${\text{C}}{{\text{N}}^ - }\, = \,\dfrac{{10 - 4}}{2}$
${\text{C}}{{\text{N}}^ - }\, = \,3$
The structure of both molecules is as follows:
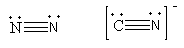
As both have the same bond order and geometry so, the energy will also be the same but the dinitrogen is a nonpolar molecule whereas due to the difference in electronegativity the cyanide is a polar molecule. The polar molecules have charge separation so the bond length of the C-N is somewhat larger than the N-N bond length.
Bon length is inversely proportional to the bond energy so, due to the smaller N-N bond length, the N-N bond energy is high, so, due to high energy requirement for the breaking of the N-N bond, the dinitrogen is unreactive or we can say chemical inert.
Therefore, option (B) larger N-N bond energy, is correct.
Note: Inertness is directly proportional to the stability and inversely proportional to the reactivity. Stability is directly proportional to the bond order which in turn directly proportional to the bond energy. Both bond energy and bond order are inversely proportional to the bond length. Stability is also directly proportional to the small size and high effective nuclear charge.
Complete step-by-step answer:
The molecular electronic configuration of ${\text{C}}{{\text{N}}^ - }$and ${{\text{N}}_{\text{2}}}$are as follows:
\[{{\text{N}}_{\text{2}}}\,{\text{ = }}{\left( {{{1s\sigma}}} \right)^{\text{2}}}{\left( {{\text{1s}}{{{\sigma}}^{\text{*}}}} \right)^{\text{2}}}{\left( {{{2s\sigma}}} \right)^{\text{2}}}{\left( {{\text{2s}}{{{\sigma}}^{\text{*}}}} \right)^{\text{2}}}{\left( {{\text{2}}{{\text{p}}_{\text{x}}}{{\pi}} \approx {\text{2}}{{\text{p}}_{\text{y}}}{{\pi}}} \right)^4}{\left( {{\text{2}}{{\text{p}}_{\text{Z}}}{{\sigma}}} \right)^2}\left( {{\text{2}}{{\text{p}}_{\text{x}}}{{{\pi}}^{\text{*}}} \approx {\text{2}}{{\text{p}}_{\text{y}}}{{{\pi}}^{\text{*}}}} \right)\left( {{\text{2}}{{\text{p}}_{\text{Z}}}{{{\sigma}}^{\text{*}}}} \right)\]
\[{\text{C}}{{\text{N}}^ - }\,{\text{ = }}{\left( {{{1s\sigma}}} \right)^{\text{2}}}{\left( {{\text{1s}}{{{\sigma}}^{\text{*}}}} \right)^{\text{2}}}{\left( {{{2s\sigma}}} \right)^{\text{2}}}{\left( {{\text{2s}}{{{\sigma}}^{\text{*}}}} \right)^{\text{2}}}{\left( {{\text{2}}{{\text{p}}_{\text{x}}}{{\pi}} \approx {\text{2}}{{\text{p}}_{\text{y}}}{{\pi}}} \right)^4}{\left( {{\text{2}}{{\text{p}}_{\text{Z}}}{{\sigma}}} \right)^2}\left( {{\text{2}}{{\text{p}}_{\text{x}}}{{{\pi}}^{\text{*}}} \approx {\text{2}}{{\text{p}}_{\text{y}}}{{{\pi}}^{\text{*}}}} \right)\left( {{\text{2}}{{\text{p}}_{\text{Z}}}{{{\sigma}}^{\text{*}}}} \right)\]
The formula to determine the bond order is as follows:
Bonding electron – Anti bonding electrons / $2$
Bond order of${{\text{N}}_{\text{2}}}$,
${{\text{N}}_{\text{2}}}\, = \,\dfrac{{10 - 4}}{2}$
${{\text{N}}_{\text{2}}}\, = \,3$
Bond order of${\text{C}}{{\text{N}}^ - }$,
${\text{C}}{{\text{N}}^ - }\, = \,\dfrac{{10 - 4}}{2}$
${\text{C}}{{\text{N}}^ - }\, = \,3$
The structure of both molecules is as follows:
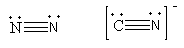
As both have the same bond order and geometry so, the energy will also be the same but the dinitrogen is a nonpolar molecule whereas due to the difference in electronegativity the cyanide is a polar molecule. The polar molecules have charge separation so the bond length of the C-N is somewhat larger than the N-N bond length.
Bon length is inversely proportional to the bond energy so, due to the smaller N-N bond length, the N-N bond energy is high, so, due to high energy requirement for the breaking of the N-N bond, the dinitrogen is unreactive or we can say chemical inert.
Therefore, option (B) larger N-N bond energy, is correct.
Note: Inertness is directly proportional to the stability and inversely proportional to the reactivity. Stability is directly proportional to the bond order which in turn directly proportional to the bond energy. Both bond energy and bond order are inversely proportional to the bond length. Stability is also directly proportional to the small size and high effective nuclear charge.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




