Question

Classify the ${118^ \circ }$ angle as acute, obtuse, straight, right, zero or complete angle.

Answer 1

Hint: An angle may be defined as the figure formed by two rays which are meeting at a common endpoint. An angle is represented by the symbol ∠. The two sides of an angle are termed as arms and the end point of the angles where the two rays are meeting is called vertex.

Complete step-by-step answer:
The broad classification of angles is given below:
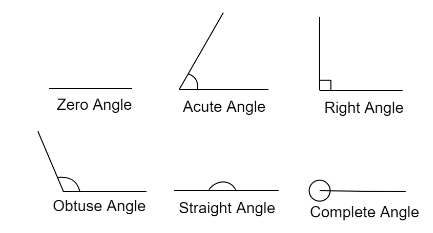
Acute angle: An acute angle refers to an angle that is less than \[{90^ \circ }\] but larger than \[{0^ \circ }\]. Therefore, an acute angle is an angle that measures between \[{0^ \circ }\] and \[{90^ \circ }\]. For examples: \[{30^ \circ }\], \[{60^ \circ }\]or \[{15^ \circ }\].
Obtuse angle: An obtuse angle is always larger than \[{90^ \circ }\] but less than \[{180^ \circ }\]. In other words, the angle that lies between \[{90^ \circ }\] and \[{180^ \circ }\] is called an obtuse angle. For example: \[{95^ \circ }\], \[{120^ \circ }\]or \[{155^ \circ }\]
Straight angle: A straight angle is the angle that is equal to \[{180^ \circ }\]. It points in the opposite way. It looks like a straight line.
Right angle: A right angle is an angle which is exactly equal to \[{90^ \circ }\]. It corresponds to a quarter of a circle.
Zero angle: The smallest angle with a measure of \[{0^ \circ }\] is called a zero angle. Here, both the arms of the angle overlaps one another.
Complete angle: A full angle or round angle, is an angle which is equal to \[{360^ \circ }\], corresponding to the central angle of an entire circle. Four right angles or two straight angles equal to one full angle.

Based upon the above classification, the given angle of ${118^ \circ }$ will be an obtuse angle as it lies between \[{90^ \circ }\] and \[{180^ \circ }\].

Note: The angles in the ascending order can be written as:
Zero angle < Acute angle < Right angle < Obtuse angle < Straight angle < Complete angle.
Zero angle is the smallest angle and complete angle is the largest angle.