Question

Circles of radii 36 and 9 touch externally. The radius of the circle which touches the two circles externally and also their common tangent is : \[\]
A. 2\[\]
B.4\[\]
C.$\sqrt{17}$\[\]
D. $\sqrt{18}$\[\]

Answer 1

Hint:We draw the diagram where A, C,O is the centre the small circle with radius 9 , the centre of the large circle radius 36 and the circle which touches both of them respectively. Their corresponding points of contact are B, G, and D. We produce AL and MN and parallel and equal to BD. We denote $BG=x,BD=d$ and the required radius$OG=r$. We use Pythagoras theorem in the triangles ALM, AON, COM to find $x,d$ and then $r.$\[\]

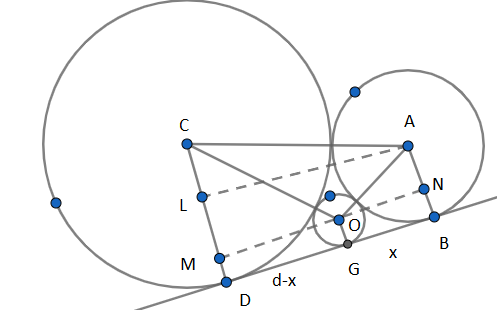
Let us denote the centre of the small circle with radius 9 as A and centre of the large circle radius 36 as C. B and D are the points of contact with their common tangent. So we have the length of the radii$AB=9,CD=36$. We denote the centre of the circle which touches both the small and large circle as O and the point of contact of this circle on the tangent is G. So its radius is OG which we denote as $r=OG$\[\]


We produce the line segment MN which passes through O and parallel and equal to BD. We also produce the line segment AL which is and parallel and equal to BD. We know that the radius of circle is perpendicular to its tangent. So BD as well as its parallel lines MN and AL will be perpendicular to both radii AB and CD.
Let us assume $BG=x,BD=d$ which implies$GD=d-x$ . We get in accordance with our construction$BD=AL=MN=d,OM=d-x,ON=x$. \[\]
We know from Pythagoras theorem that “In a right-angled triangle the square of hypotenuse is sum of squares of other two sides.” So we have in the right-angled triangle ALC We know that distance between centres is the sum of radii, so$AC=AB+CD=36+9=45$. We also have$CL=CD-LM=CD-AB=36-9=27.$ We use the Pythagoras theorem and have,

\[\begin{align}
  & A{{C}^{2}}=C{{L}^{2}}+A{{L}^{2}} \\
 & \Rightarrow A{{L}^{2}}=A{{C}^{2}}-C{{L}^{2}} \\
 & \Rightarrow {{d}^{2}}={{45}^{2}}-{{36}^{2}} \\
 & \Rightarrow {{d}^{2}}=1296 \\
 & \Rightarrow d=36 \\
\end{align}\]
 We see in the right-angled triangle AON, $AO=9+OG=9+r$ and $AN=AB-NB=AB-OG=9-r$. We use the Pythagoras theorem and have
\[\begin{align}
  & A{{O}^{2}}=A{{N}^{2}}+O{{N}^{2}} \\
 & \Rightarrow {{\left( 9+r \right)}^{2}}={{\left( 9-r \right)}^{2}}+{{x}^{2}} \\
 & \Rightarrow {{x}^{2}}=4\times 9\times r=36r \\
 & \Rightarrow x=6\sqrt{r} \\
\end{align}\]
We see in the right-angled triangle COM, $CO=CD+OG=36+r$ and $CM=CD-DM=CD-OG=36-r$. We use the Pythagoras theorem and have
\[\begin{align}
  & C{{O}^{2}}=C{{M}^{2}}+O{{M}^{2}} \\
 & \Rightarrow {{\left( 36+r \right)}^{2}}={{\left( 36-r \right)}^{2}}+{{\left( d-x \right)}^{2}} \\
 & \Rightarrow {{\left( d-x \right)}^{2}}=4\times 36\times r=144r \\
 & \Rightarrow d-x=12\sqrt{r} \\
\end{align}\]
We put previously obtained $x=6\sqrt{r},d=36$ and have,
\[\begin{align}
  & 36-6\sqrt{r}=12\sqrt{r} \\
 & \Rightarrow \sqrt{r}=\dfrac{36}{18}=2 \\
 & \Rightarrow r=4 \\
\end{align}\]
So the radius of the circle which touches the two circles externally and also their common tangent is 4 and the correct option is B.\[\]

Note:
We have rejected the negative square root everywhere because distance is positive quantity. We can directly find radius $r$ of the circle which touches two other circles with radii ${{r}_{1}},{{r}_{2}}$ using the formula $\dfrac{1}{\sqrt{r}}=\dfrac{1}{\sqrt{{{r}_{1}}}}+\dfrac{1}{\sqrt{{{r}_{2}}}}$.