Question

Circles \[{{C}_{1}}\] and \[{{C}_{2}}\] are extremely tangent and they both internally tangent to the circle \[{{C}_{3}}\]. The radii of \[C_{1}^{{}}\] and \[{{C}_{2}}\] are \[4\] and \[10\], respectively and the centers of the three circles are collinear. A chord of \[{{C}_{3}}\] is also a common internal of
\[{{C}_{1}}\] and \[{{C}_{2}}\]. Given that the length of the chord is \[\dfrac{m\sqrt{n}}{p}\] where
\[m,\text{ }n\]and \[p\] are positive integers, \[m\] and \[p\] are relative prime and n is not divisible by the square of any prime, find the value of \[\left( m+n+p \right)\].

Answer 1

Hint:According to the question, to find the value of \[\left( m+n+p \right)\], we need to equate the triangles
\[XOT,X{{O}_{1}}{{T}_{1}},X{{O}_{2}}{{T}_{2}}\] as shown in the diagram below:

find the tangent length going over
\[{{O}_{1}},{{O}_{2}}\].

Complete step by step solution:
First let us mark the center of the triangles as \[O,{{O}_{1}},{{O}_{2}}\] and the radius of the three circles as:
\[r1=4\], \[r2=10\] and \[r3=14\]

Now let us draw a diagram of the circles along with their radius and the point where \[{{C}_{1}}\] and
\[{{C}_{2}}\] are touching the tangent on the edge of the circle.

The diagram also includes the point where the extension of radiuses of all the circles and tangents intersect and is marked as \[X\].

Now using the triangle’s similarity we equate the following triangles
\[XOT,X{{O}_{1}}{{T}_{1}},X{{O}_{2}}{{T}_{2}}\] to find the value of the line \[{{O}_{1}}{{T}_{1}}\].

Hence equating the lines in ratio of:
\[\dfrac{XO}{OT}=\dfrac{X{{O}_{2}}}{{{O}_{2}}{{T}_{2}}}=\dfrac{X{{O}_{1}}}{{{O}_{1}}{{T}_{1}}}\]
Placing the value of \[OT\] and \[{{O}_{2}}{{T}_{2}}\] as \[4\] and \[10\] and replacing the values of

\[X{{O}_{1}}\] and \[X{{O}_{2}}\] in terms of \[X{{O}_{1}}\] as \[XP+14\] and \[X{{O}_{2}}\] as \[XP+18\].
\[\Rightarrow \dfrac{XP+4}{4}=\dfrac{XP+14}{{{O}_{1}}{{T}_{1}}}=\dfrac{XP+18}{10}\]
\[\Rightarrow \dfrac{4\left( XP+14 \right)}{XP+4\left( {{O}_{1}}{{T}_{1}} \right)}=\dfrac{XP+18}{10}\]

Cross multiplying the values in the ratio we get the value of \[XO\] and \[{{O}_{1}}{{T}_{1}}\] as:
\[\Rightarrow \dfrac{XP}{{{O}_{1}}{{T}_{1}}}=\dfrac{\dfrac{16}{3}}{\dfrac{58}{7}}\]
After getting the values of \[XP\] and \[{{O}_{1}}{{T}_{1}}\] we find the value of \[B{{T}_{1}}\] as shown in the diagram below:

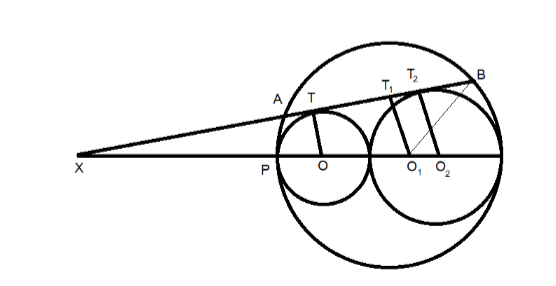
Using Pythagoras Theorem, we find the value of \[BO\] as:

\[\Rightarrow B{{T}_{1}}^{2}={{O}_{1}}{{T}_{1}}^{2}-{{\left( 3XP \right)}^{2}}\]
\[\because \] The value of XP is three times as the lines are cut into three equal parts.
\[\Rightarrow B{{T}_{1}}=\sqrt{{{\left( 3\times \dfrac{16}{3} \right)}^{2}}-{{\left( \dfrac{58}{7}
\right)}^{2}}}\]
\[\Rightarrow B{{T}_{1}}=\sqrt{194-{{\left( \dfrac{58}{7} \right)}^{2}}}\]
\[\Rightarrow B{{T}_{1}}=\dfrac{8}{7}\sqrt{390}\]

Now comparing the value of \B{{T}_{1}}\ by the value of \[\dfrac{m\sqrt{n}}{p}\], we get the values of
\[m,n,p\] as \[8,390,7\] respectively.

Therefore, the sum of the value of \[\left( m+n+p \right)\] is \[8+390+7=405\].

Note:Students may go wrong in various places like when taking the tangent measurement and when taking the radius of the third circle one must remember that we do have all the radius and by drawing diagram we make three triangles with P as one of the corners for all the three triangles once getting two sides of all the triangles we move to find the distance between the two tangent points which form the chord of the circle. A chord is a line which cuts the circle into two with one side greater than half and another side less than half.