Question

Choose and write the correct option in each of the following questions:
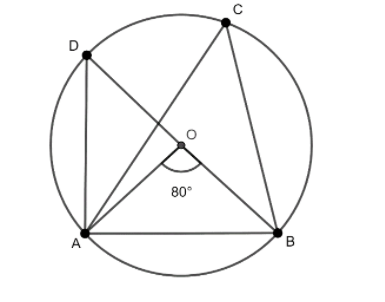
In the figure, if O is the centre of a circle, then the measure of $\angle ADB$ is:
a. $80^\circ $
b. $100^\circ $
c. $40^\circ $
d. $60^\circ $

Answer 1

Hint: We can use the exterior angle of the triangle \[\vartriangle DOA\] to find the interior angle $\angle ADO$ as we know the exterior angle $\angle AOB$. We will use the fact that both $AO$ and $DO$ are radii of the circle as $O$ is the center to find the relationship between the interior angles.

Complete step-by-step answer:
In the given figure we have to find the value of the angle $\angle ADB$. Observe that the angle is contained in two triangles $\vartriangle ADB$ and $\vartriangle ADO$. We will consider the triangle $\vartriangle ADO$ as the angle $\angle AOB$ whose value is given to be $80^\circ $ is an exterior angle of this triangle. WE use the exterior angle property with respect to the exterior angle $\angle AOB$.
Let us consider $\angle ADB$ to be $x$. Recall that the exterior angle property of a triangle states that the exterior angle of a triangle is equal to the sum of two opposite interior angles. Using this property, we can see that in $\vartriangle ADO$, the exterior angle $\angle AOB$ is equal to the sum of $\angle ADO$ and $\angle DAO$.
$ \Rightarrow \angle AOB = \angle ADO + \angle DAO$
$ \Rightarrow \angle ADO + \angle DAO = 80^\circ $ - - - - - - - - - - - - - - (1)
Now since both $AO$ and $DO$ are radii of the circle as $O$ is the center of the circle, we can see that $AO = DO$.
We know the property that angles opposite to equal sides are equal. So, by using this and since $AO = DO$, we have the angles opposite to these sides $\angle ADO$ and $\angle DAO$ to be equal, that is $\angle ADO = \angle DAO$. - - - - - - - - - - - - - - - (2)
Now by using (2), we can write the equation (1) as,
$ \Rightarrow \angle ADO + \angle ADO = 80^\circ $
$ \Rightarrow 2\angle ADO = 80^\circ $
$ \Rightarrow \angle ADO = \dfrac{{80^\circ }}{2}$
$ \Rightarrow \angle ADO = 40^\circ $
$ \Rightarrow \angle ADB = 40^\circ $ [From the figure we have $\angle ADO = \angle ADB$]
So, the measure of the angle $\angle ADB$ is $40^\circ $.
Hence, the correct option is C. $40^\circ $.
So, the correct answer is “Option C”.

Note: There are multiple ways of solving this question. One way is to use the angle sum property of a triangle for the triangles $\vartriangle AOB$ and $\vartriangle ADB$ along with using the property of an isosceles triangle. One has to know all the properties related to triangles and circles to solve questions from geometry.