Question

How many children will a school hall of dimensions 20 m, 9.5 m and 8 m high accommodate, assuming \[2.5{{m}^{3}}\] of air required for each child?

Answer 1

Hint: We will find the volume of a school hall then by using the unitary method we will find the number of children required. We will use the formula to find the volume of the school hall since it is a cuboid. So the volume of cuboid having length (l), breadth (b) and height (h) is given by:
Volume \[=l\times b\times h\] cubic unit

Complete step-by-step answer:
We have been asked to find the number of children accommodated in a school hall of dimensions 20 m, 9.5 m and 8 m high by assuming \[2.5{{m}^{3}}\] of air required by each child.
Since a school hall is in the form of cuboid and we know that the volume of cuboid having dimensions l, b and h is given by:
Volume \[=l\times b\times h\] cubic unit

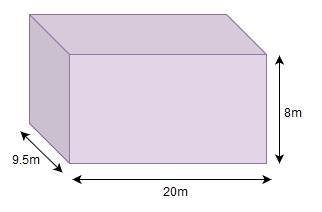
So the volume of school hall of dimensions 20 m, 9.5 m and 8 m is given by:
Volume of school hall = volume of air \[=20\times 9.5\times 8=1520{{m}^{3}}\]
Since we have been given \[2.5{{m}^{3}}\] of air required for each child
\[\Rightarrow 2.5{{m}^{3}}\] air for one child
In \[1{{m}^{3}}\] of air, number of children \[=\dfrac{1}{2.5}\]
So, in \[1520{{m}^{3}}\] of air, number of children \[=1520\times \dfrac{1}{2.5}=608\]
Therefore, the required number of children is equal to 608.

Note: Be careful while doing calculation, if we were given the dimensions of the hall in different units, then we should have converted them to a single unit. Some students get confused when they read the question with details of volume of air for each child. So, they must remember that the volume of any object or a substance is the space that a substance or an object occupies or the space that is enclosed within a container. So, here it means that each child occupies that much space of the total volume.