Question

Check which of the following are the solutions of the equation $5x - 4y = 20$.
(A) $(4,0)$
(B) $(0,5)$
(C) $\left( { - 2,\dfrac{5}{2}} \right)$
(D) $\left( {0, - 5} \right)$
(E) $\left( {2,\dfrac{5}{2}} \right)$

Answer 1

Hint: Here we have to put the value of x and y in the given equation one by one and then we have to check which option we are getting on the left hand side equals the right hand side. In the given options the value before the comma represents the value of x coordinate and the value after the comma represents the value of y coordinate.

Complete step by step answer:
In the above question, it is given that $5x - 4y = 20$.
Now we will take all the options one by one and put the coordinates in the given equation and check which option we are getting on the left hand side equals the right hand side.
In option (A)
We have coordinates $(4,0)$ in which the value of x is $4$ and the value of y is $0$.
On putting the above coordinates in the given equation, we get
 $5\left( 4 \right) - 4\left( 0 \right) = 20$
$ \Rightarrow 20 = 20$
Therefore, we have the same values on both the left-hand side and right-hand side.
Hence, the option (A) is correct.
In option (B)
We have coordinates $(0,5)$ in which the value of x is $0$ and the value of y is $5$.
On putting the above coordinates in the given equation, we get
 $5\left( 0 \right) - 4\left( 5 \right) = 20$
$ \Rightarrow - 20 \ne 20$
Therefore, we have different values in both the left-hand side and right-hand side.
Hence, the option (B) is incorrect.
In option (C)
We have coordinates $\left( { - 2,\dfrac{5}{2}} \right)$ in which the value of x is $ - 2$ and the value of y is $\dfrac{5}{2}$.
On putting the above coordinates in the given equation, we get
 $5\left( { - 2} \right) - 4\left( {\dfrac{5}{2}} \right) = 20$
On simplification, we get
$ \Rightarrow - 20 \ne 20$
Therefore, we have different values in both the left-hand side and right-hand side.
Hence, the option (C) is incorrect.
In option (D)
We have coordinates $(0, - 5)$ in which the value of x is $0$ and the value of y is $ - 5$.
On putting the above coordinates in the given equation, we get
 $5\left( 0 \right) - 4\left( { - 5} \right) = 20$
$ \Rightarrow 20 = 20$
Therefore, we have the same value in both the left-hand side and right-hand side.
Hence, the option (D) is correct.
In option (E)
We have coordinates $\left( {2,\dfrac{5}{2}} \right)$ in which the value of x is $2$ and the value of y is $\dfrac{5}{2}$.
On putting the above coordinates in the given equation, we get
 $5\left( 2 \right) - 4\left( {\dfrac{5}{2}} \right) = 20$
On simplification, we get
$ \Rightarrow 0 \ne 20$
Therefore, we have different values in both the left-hand side and right-hand side.
Hence, the option (E) is incorrect.
Therefore, option (A) and (D) are correct.

Note:
The above equation is a linear equation in two variables. It also represents a straight line on graph. All the points which are satisfying the above equation lie on the line and all those points which are not satisfying the above equation do not lie on that line.
We can see the graph of the line $5x-4y=20$ (in red color) along with the points (green color) given in the options.

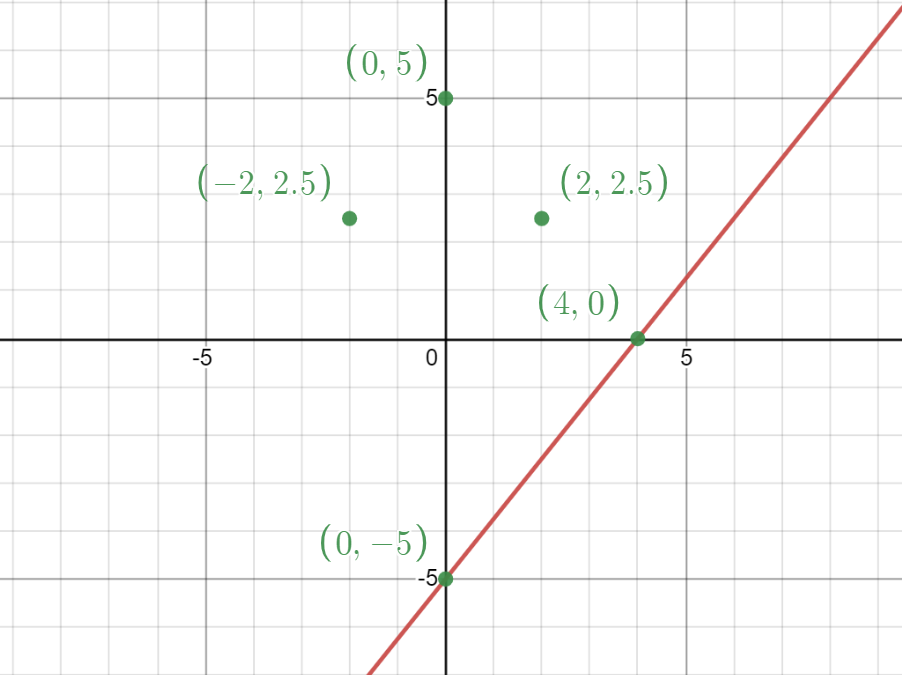
From the graph it is clear that only $(0,-5)$ and $(4,0)$ are lying on the line and they will be solutions.