Question

Check whether the following equations are consistent or inconsistent. Solve them graphically:
3x+2y=5
2x-3y=7

Answer 1

Hint: This question is from the topic of linear equations in two variables. In solving this question, we will first know about the term consistent and inconsistent by using the two different linear equations of two variables. After that, we will check if the equation 3x+2y=5 and the equation 2x-3y=7 is consistent or inconsistent. After that, we will solve the given equations graphically.

Complete step by step solution:
Let us solve this question.
In this question, we have asked to check whether the given equations are consistent or inconsistent. The given equations are:
3x+2y=5
2x-3y=7
So, let us first understand about the terms consistent and inconsistent.
Let us understand this by using two different linear equations having two variables.
\[{{a}_{1}}x+{{b}_{1}}y={{c}_{1}}\]
And \[{{a}_{2}}x+{{b}_{2}}y={{c}_{2}}\]
The term consistent means both the equations are having one solution or infinite solutions. And the term inconsistent means both the equations are having no solutions.
Condition for one (or unique) solution is: \[\dfrac{{{a}_{1}}}{{{a}_{2}}}\ne \dfrac{{{b}_{1}}}{{{b}_{2}}}\]
The condition for infinite solutions is: \[\dfrac{{{a}_{1}}}{{{a}_{2}}}=\dfrac{{{b}_{1}}}{{{b}_{2}}}=\dfrac{{{c}_{1}}}{{{c}_{2}}}\]
And, the condition for no solutions is: \[\dfrac{{{a}_{1}}}{{{a}_{2}}}=\dfrac{{{b}_{1}}}{{{b}_{2}}}\ne \dfrac{{{c}_{1}}}{{{c}_{2}}}\]
So, from the equations 3x+2y=5 and 2x-3y=7, we can say that
\[\dfrac{{{a}_{1}}}{{{a}_{2}}}=\dfrac{3}{2}\], \[\dfrac{{{b}_{1}}}{{{b}_{2}}}=\dfrac{2}{-3}=-\dfrac{2}{3}\], and \[\dfrac{{{c}_{1}}}{{{c}_{2}}}=\dfrac{5}{7}\].
From here, we can say that \[\dfrac{{{a}_{1}}}{{{a}_{2}}}\ne \dfrac{{{b}_{1}}}{{{b}_{2}}}\].
We know that if \[\dfrac{{{a}_{1}}}{{{a}_{2}}}\ne \dfrac{{{b}_{1}}}{{{b}_{2}}}\], then the equations have unique solution.
Hence, we can say that the given equations are consistent.
Now, let us understand this graphically.

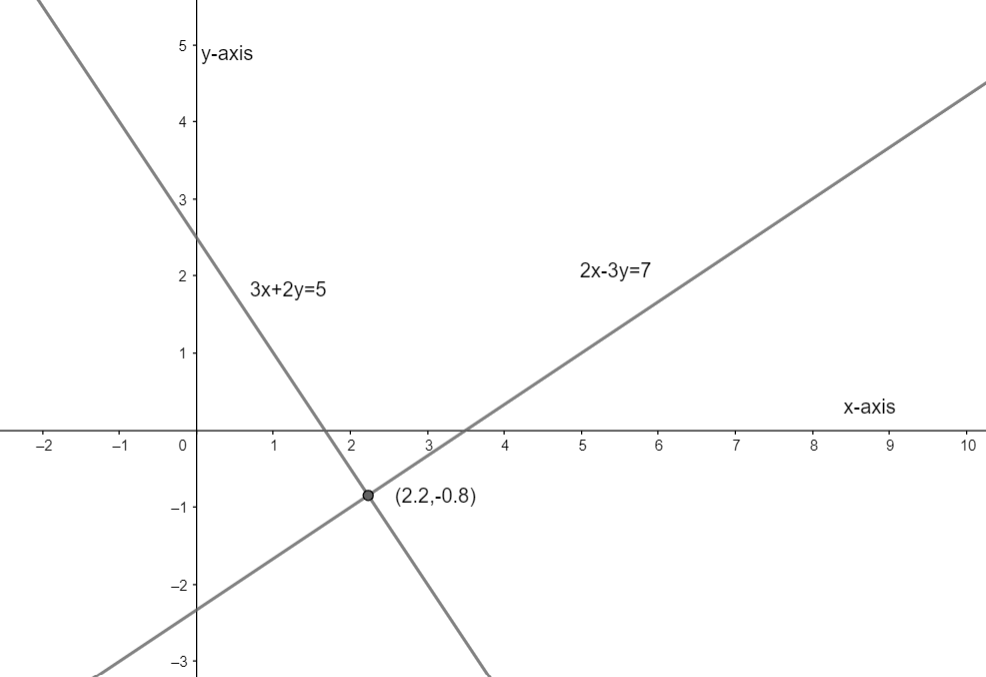
Note: We should have a better knowledge in the topic of linear equations in two variables to solve this type of question easily. We should know about the term consistent and inconsistent. Remember that the term consistent means two linear equations are having unique solution or infinite solutions. And the term inconsistent means two linear equations are having no solutions.
Suppose, we have given two equations as \[{{a}_{1}}x+{{b}_{1}}y={{c}_{1}}\] and \[{{a}_{2}}x+{{b}_{2}}y={{c}_{2}}\]
Then, the condition for
1) unique solution is \[\dfrac{{{a}_{1}}}{{{a}_{2}}}\ne \dfrac{{{b}_{1}}}{{{b}_{2}}}\]
2) infinite solutions is \[\dfrac{{{a}_{1}}}{{{a}_{2}}}=\dfrac{{{b}_{1}}}{{{b}_{2}}}=\dfrac{{{c}_{1}}}{{{c}_{2}}}\]
3) no solutions is \[\dfrac{{{a}_{1}}}{{{a}_{2}}}=\dfrac{{{b}_{1}}}{{{b}_{2}}}\ne \dfrac{{{c}_{1}}}{{{c}_{2}}}\]