Question

Check whether for the value of some angle $A$ is it possible that value of $\sec A=\dfrac{12}{5}$. Enter 1 for true and 0 for false.

Answer 1

Hint: For solving this question first we will find the value of $\cos A$ from the given value of $\sec A=\dfrac{12}{5}$ with the help of the equation $\sec A=\dfrac{1}{\cos A}$ . After that, we will consider a $\Delta ABC$ and from the basic definition of $\cos A=\dfrac{base}{hypotenuse}$ we will check whether the given data is true or not.

Complete Step-by-Step solution:
Given:
We have to check whether for the value of some angle $A$ is it possible that value of $\sec A=\dfrac{12}{5}$ .
Now, as we know that $\sec A=\dfrac{1}{\cos A}$ and it is given that $\sec A=\dfrac{12}{5}$ . Then, the value of $\cos A=\dfrac{5}{12}$ .
Now, we will proceed as per the definition of $\cos A$ and check whether it is possible or not that $\cos A=\dfrac{5}{12}$ .
Now, consider $\Delta ABC$ in which $\angle BAC=\angle A$ and $\angle ABC={{90}^{0}}$ . For more clarity look at the figure given below:

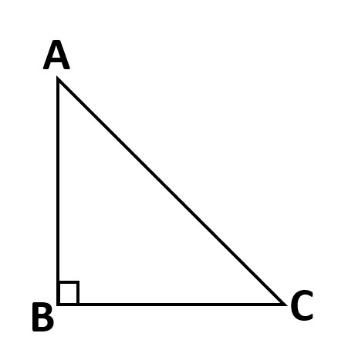
Now, as per the definition value $\cos A=\dfrac{base}{hypotenuse}=\dfrac{AB}{AC}$ and we know that in a right-angle triangle length of the hypotenuse is the highest. So, we conclude that the value of $\cos A$ will be less than 1 always.
Now, in our problem, it is given that $\sec A=\dfrac{12}{5}$ or $\cos A=\dfrac{5}{12}$ . And from the above discussion we conclude that as the value of $\cos A=\dfrac{5}{12}$ which is less than one so, the given data is true.
Thus, we conclude that for some angle $A$ it is possible that value of $\sec A=\dfrac{12}{5}$ so, we will enter 1 for our final answer.

Note: Here, the student should first understand what is asked in the problem. After that, we should use the basics of trigonometry properly and an important property of the right-angle triangle is that the hypotenuse will be more than the length of the base. Moreover, we should solve this question very carefully as these conceptual problems will help us in building our basic concepts of trigonometry.