
Charges $25 \mathrm{Q}, 9 \mathrm{Q}$ and $\mathrm{Q}$ are placed at point $\mathrm{ABC}$ such that $\mathrm{AB}=4 \mathrm{~m}, \mathrm{BC}=3 \mathrm{~m}$ and angle between $\mathrm{AB}$ and $\mathrm{BC}$ is $90^{\circ} .$ then force on the charge $\mathrm{C}$ is:
A. zero
B.$\dfrac{{{q}^{2}}}{\pi {{\in }_{0}}\sqrt{5}}$
C. $\dfrac{2{{\text{Q}}^{2}}}{\pi \in \theta }$
D.\[\dfrac{5{{Q}^{2}}}{4\pi \in }0\]
Answer
571.8k+ views
Hint: If the electrical field is known, then the electrostatic force on any charge q is obtained simply by multiplying the electrical field charging times. Throughout space, the Coulomb force field surrounding any charge extends. For a point charge (a particle having a charge Q) at a distance r acting on a test charge q. Q and the test charge q are dependent on both the magnitude and direction of the Coulomb force field.
Complete answer:
Coulomb's Law Equation where $\mathrm{q}_{1}\left(\mathrm{ie} \mathrm{F}_{31}\right)$ is the amount of charge on object 1 (in Coulombs), ${{\text{q}}_{2}}$ is the amount of charge on object 2 (in Coulombs), and d is the distance of separation (in meters) between the two objects. The symbol k is a constant of proportionality known as the constant of Coulomb's law.
Let us define,
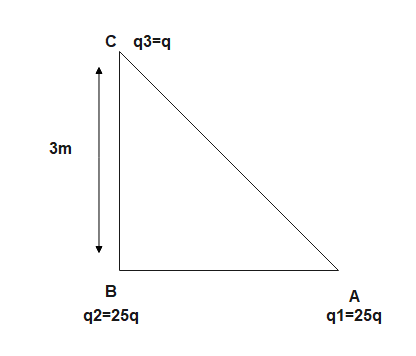
According to question
$\mathrm{q}_{1}=25 ; \mathrm{q}_{2}=9 \mathrm{q} ; \mathrm{q}_{3}=\mathrm{q}$ placed at $\mathrm{A}, \mathrm{B}$ and $\mathrm{C}$ respectively
The total force on $\mathrm{q}_{3}$ will be the vector sum of force on $\mathrm{q}_{3}$ due to $\mathrm{q}_{2}$ (i.e. $\mathrm{F}_{32}$ ) and force on $\mathrm{q}_{3}$ due to i.e. $\mathrm{q}_{1}\left(\mathrm{ie} \mathrm{F}_{31}\right)$
${{\text{F}}_{32}}=\dfrac{{{\text{q}}_{3}}{{\text{q}}_{2}}}{4\pi {{\epsilon }_{0}}{{(\text{BC})}^{2}}}$
$\Rightarrow \dfrac{9{{\text{q}}^{2}}}{4\pi {{\epsilon }_{0}}\times 9}=\dfrac{{{\text{q}}^{2}}}{4\pi {{\epsilon }_{0}}}$
${{\text{F}}_{31}}=\dfrac{{{\text{q}}_{3}}{{\text{q}}_{1}}}{4\pi {{\epsilon }_{0}}\left( {{(\text{AB})}^{2}}+{{(\text{BC})}^{2}} \right)}$
$\Rightarrow \dfrac{25{{\text{q}}^{2}}}{4\pi {{\epsilon }_{0}}\times 25}=\dfrac{{{\text{q}}^{2}}}{4\pi {{\epsilon }_{0}}}$
$\mathrm{F}_{\text {total }}=\sqrt{\mathrm{F}_{32}^{2}+\mathrm{F}_{31}^{2}+2 \mathrm{F}_{32} \mathrm{F}_{31} \cos \theta}$
here, $\cos \theta=\dfrac{3}{5}$
$\Rightarrow \mathrm{F}_{\text {total }}=\dfrac{\mathrm{q}^{2}}{4 \pi \epsilon_{0}} \sqrt{1+1+2 \times \dfrac{3}{5}}$
$\therefore {{\text{F}}_{\text{total }}}=\dfrac{{{\text{q}}^{2}}}{\sqrt{5}\pi {{\epsilon }_{0}}}$
The force on the charge $\mathrm{C}$ is: $\Rightarrow \mathrm{F}_{\text {total }}=\dfrac{\mathrm{q}^{2}}{\sqrt{5} \pi \epsilon_{0}}$
The correct option is (B).
Note:
Therefore, it is seen that the electric field depends only on the charge Q and the distance r; it is completely independent of the test charge q. The charges are typical of common static electricity in this example, and the modest repulsive force obtained is comparable to forces experienced in static clinging and similar situations
Complete answer:
Coulomb's Law Equation where $\mathrm{q}_{1}\left(\mathrm{ie} \mathrm{F}_{31}\right)$ is the amount of charge on object 1 (in Coulombs), ${{\text{q}}_{2}}$ is the amount of charge on object 2 (in Coulombs), and d is the distance of separation (in meters) between the two objects. The symbol k is a constant of proportionality known as the constant of Coulomb's law.
Let us define,

According to question
$\mathrm{q}_{1}=25 ; \mathrm{q}_{2}=9 \mathrm{q} ; \mathrm{q}_{3}=\mathrm{q}$ placed at $\mathrm{A}, \mathrm{B}$ and $\mathrm{C}$ respectively
The total force on $\mathrm{q}_{3}$ will be the vector sum of force on $\mathrm{q}_{3}$ due to $\mathrm{q}_{2}$ (i.e. $\mathrm{F}_{32}$ ) and force on $\mathrm{q}_{3}$ due to i.e. $\mathrm{q}_{1}\left(\mathrm{ie} \mathrm{F}_{31}\right)$
${{\text{F}}_{32}}=\dfrac{{{\text{q}}_{3}}{{\text{q}}_{2}}}{4\pi {{\epsilon }_{0}}{{(\text{BC})}^{2}}}$
$\Rightarrow \dfrac{9{{\text{q}}^{2}}}{4\pi {{\epsilon }_{0}}\times 9}=\dfrac{{{\text{q}}^{2}}}{4\pi {{\epsilon }_{0}}}$
${{\text{F}}_{31}}=\dfrac{{{\text{q}}_{3}}{{\text{q}}_{1}}}{4\pi {{\epsilon }_{0}}\left( {{(\text{AB})}^{2}}+{{(\text{BC})}^{2}} \right)}$
$\Rightarrow \dfrac{25{{\text{q}}^{2}}}{4\pi {{\epsilon }_{0}}\times 25}=\dfrac{{{\text{q}}^{2}}}{4\pi {{\epsilon }_{0}}}$
$\mathrm{F}_{\text {total }}=\sqrt{\mathrm{F}_{32}^{2}+\mathrm{F}_{31}^{2}+2 \mathrm{F}_{32} \mathrm{F}_{31} \cos \theta}$
here, $\cos \theta=\dfrac{3}{5}$
$\Rightarrow \mathrm{F}_{\text {total }}=\dfrac{\mathrm{q}^{2}}{4 \pi \epsilon_{0}} \sqrt{1+1+2 \times \dfrac{3}{5}}$
$\therefore {{\text{F}}_{\text{total }}}=\dfrac{{{\text{q}}^{2}}}{\sqrt{5}\pi {{\epsilon }_{0}}}$
The force on the charge $\mathrm{C}$ is: $\Rightarrow \mathrm{F}_{\text {total }}=\dfrac{\mathrm{q}^{2}}{\sqrt{5} \pi \epsilon_{0}}$
The correct option is (B).
Note:
Therefore, it is seen that the electric field depends only on the charge Q and the distance r; it is completely independent of the test charge q. The charges are typical of common static electricity in this example, and the modest repulsive force obtained is comparable to forces experienced in static clinging and similar situations
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




