Question

Charges $25 \mathrm{Q}, 9 \mathrm{Q}$ and $\mathrm{Q}$ are placed at point $\mathrm{ABC}$ such that $\mathrm{AB}=4 \mathrm{~m}, \mathrm{BC}=3 \mathrm{~m}$ and angle between $\mathrm{AB}$ and $\mathrm{BC}$ is $90^{\circ} .$ then force on the charge $\mathrm{C}$ is:
A. zero
B.$\dfrac{{{q}^{2}}}{\pi {{\in }_{0}}\sqrt{5}}$
C. $\dfrac{2{{\text{Q}}^{2}}}{\pi \in \theta }$
D.\[\dfrac{5{{Q}^{2}}}{4\pi \in }0\]

Answer 1

Hint: If the electrical field is known, then the electrostatic force on any charge q is obtained simply by multiplying the electrical field charging times. Throughout space, the Coulomb force field surrounding any charge extends. For a point charge (a particle having a charge Q) at a distance r acting on a test charge q. Q and the test charge q are dependent on both the magnitude and direction of the Coulomb force field.

Complete answer:
Coulomb's Law Equation where $\mathrm{q}_{1}\left(\mathrm{ie} \mathrm{F}_{31}\right)$ is the amount of charge on object 1 (in Coulombs), ${{\text{q}}_{2}}$ is the amount of charge on object 2 (in Coulombs), and d is the distance of separation (in meters) between the two objects. The symbol k is a constant of proportionality known as the constant of Coulomb's law.
Let us define,

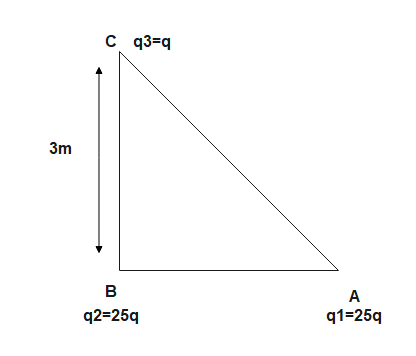
According to question
$\mathrm{q}_{1}=25 ; \mathrm{q}_{2}=9 \mathrm{q} ; \mathrm{q}_{3}=\mathrm{q}$ placed at $\mathrm{A}, \mathrm{B}$ and $\mathrm{C}$ respectively
The total force on $\mathrm{q}_{3}$ will be the vector sum of force on $\mathrm{q}_{3}$ due to $\mathrm{q}_{2}$ (i.e. $\mathrm{F}_{32}$ ) and force on $\mathrm{q}_{3}$ due to i.e. $\mathrm{q}_{1}\left(\mathrm{ie} \mathrm{F}_{31}\right)$
${{\text{F}}_{32}}=\dfrac{{{\text{q}}_{3}}{{\text{q}}_{2}}}{4\pi {{\epsilon }_{0}}{{(\text{BC})}^{2}}}$
$\Rightarrow \dfrac{9{{\text{q}}^{2}}}{4\pi {{\epsilon }_{0}}\times 9}=\dfrac{{{\text{q}}^{2}}}{4\pi {{\epsilon }_{0}}}$
${{\text{F}}_{31}}=\dfrac{{{\text{q}}_{3}}{{\text{q}}_{1}}}{4\pi {{\epsilon }_{0}}\left( {{(\text{AB})}^{2}}+{{(\text{BC})}^{2}} \right)}$
$\Rightarrow \dfrac{25{{\text{q}}^{2}}}{4\pi {{\epsilon }_{0}}\times 25}=\dfrac{{{\text{q}}^{2}}}{4\pi {{\epsilon }_{0}}}$
$\mathrm{F}_{\text {total }}=\sqrt{\mathrm{F}_{32}^{2}+\mathrm{F}_{31}^{2}+2 \mathrm{F}_{32} \mathrm{F}_{31} \cos \theta}$
here, $\cos \theta=\dfrac{3}{5}$
$\Rightarrow \mathrm{F}_{\text {total }}=\dfrac{\mathrm{q}^{2}}{4 \pi \epsilon_{0}} \sqrt{1+1+2 \times \dfrac{3}{5}}$
$\therefore {{\text{F}}_{\text{total }}}=\dfrac{{{\text{q}}^{2}}}{\sqrt{5}\pi {{\epsilon }_{0}}}$
The force on the charge $\mathrm{C}$ is: $\Rightarrow \mathrm{F}_{\text {total }}=\dfrac{\mathrm{q}^{2}}{\sqrt{5} \pi \epsilon_{0}}$

The correct option is (B).

Note:
Therefore, it is seen that the electric field depends only on the charge Q and the distance r; it is completely independent of the test charge q. The charges are typical of common static electricity in this example, and the modest repulsive force obtained is comparable to forces experienced in static clinging and similar situations