Question

Centre of circle whose normal are \[{{x}^{2}}-2xy-3x+6y=0\], is
(a) $3,\dfrac{3}{2}$
(b) $3,-\dfrac{3}{2}$
(c) $\dfrac{3}{2},3$
(d) None of these

Answer 1

Hint: Given an equation of a pair of straight lines. So, that represents a pair of lines which are normal to the given circle. As we know that normal to the circle passes through the center. This point can be known to one with basic knowledge of properties of circles. If not, try to prove that and using that condition we can say that normal passes through the center. Any 2 lines which are neither coincident nor parallel they must be intersecting at only 1 point. So, the intersection point of these pair of straight lines is the center.

Complete step-by-step answer:
Proof of normal passes through center:
Normal is defined as the line perpendicular to tangent passing through the point of contact.
So, if we prove the radius line from center to point of contact is perpendicular to tangent it will indirectly prove our result. Let’s take a circle with tangent AB at P and center O and let us assume some random point X. if we take XP is perpendicular to AB.

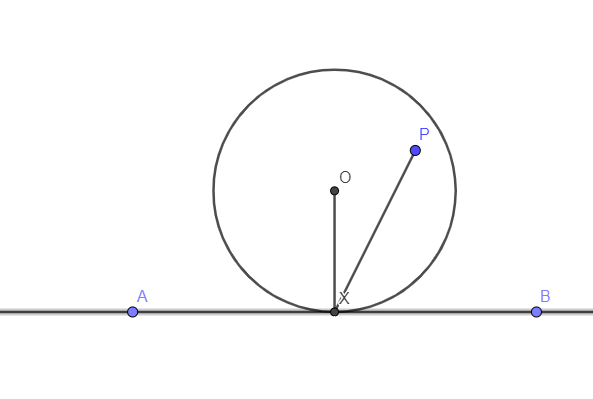
$\angle XPB=90{}^\circ $
As we already know $\angle OPB=90{}^\circ $
This case is possible only when O lies on XP.
By this we can say that normal always passes through the center.
 For first intersection point of straight lines we need to solve that equation and find roots:
Given equation in question:
\[{{x}^{2}}-2xy-3x+6y=0\]
By taking x common in first two terms of equation, we get:
$x\left( x-2y \right)-3x+6y=0$
By taking -3 common in last two terms of equation, we get:
$x\left( x-2y \right)-3\left( x-2y \right)=0$
By taking $\left( x-2y \right)$ term common in the above equation, we get:
$\left( x-2y \right)\left( x-3 \right)=0$
So, $x-3=0$ and $x-2y=0$ are equations of both the normals.
From first line, we get: \[x=3\ldots \ldots ..\left( i \right)\]
By substituting this into the second normal, we get:
$3-2y=0$
By simplifying this equation, we get:
$\begin{align}
  & y=\dfrac{3}{2}.........(ii) \\
 & \\
\end{align}$
From equation (i) and (ii) we say:
Centre= $3,\dfrac{3}{2}$
So, the point $3,\dfrac{3}{2}$ is the centre of the circle.
Therefore option (a) is correct.

Note: Be careful while solving a pair of lines to get the equations of normal if you miss negative sign of 3 while taking common you will get a wrong equation. The whole answer might change a lot. The idea of proving line perpendicular will pass through the center is crucial.