Question

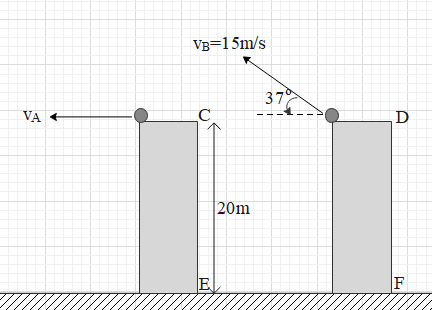
CE and DF are two walls of equal height (20meter) from which two particles A and B of same mass are projected as shown in the figure. A is projected horizontally towards left while B is projected at an angle ${{37}^{\circ }}$ (with horizontal towards left) with velocity 15 m/s. If A always sees B to be moving perpendicular to EF, then the range of A on ground is

A. 24m
B. 30m
C. 26m
D. 28m

Answer 1

Hint: It is given that the relative velocity of particle B with respect to particle A is always vertical. This means that the horizontal velocities of both the particles are equal. Then find the time of flight of A with one of the kinematic equations. With this time find the range of the A.

Complete step by step answer:
It is given that particle A always sees particle B perpendicular to EF. This tells us that the relative velocity of particle B with respect to particle A is always in the direction perpendicular to EF. Since EF is parallel to the ground, the relative velocity B with respect to A is in the vertical direction.
We know that particle B will have some velocity in the horizontal direction too. However, according to particle A, this velocity is zero. When two particles have same velocities, the relative velocity will be zero.
Therefore, the horizontal velocities of both the particles are equal.
Let us find the horizontal of particle B.
From the figure we get that the horizontal component of velocity of B is $15\cos {{37}^{\circ }}=15\times \dfrac{4}{5}=12m{{s}^{-1}}$.
This means that ${{v}_{A}}=12m{{s}^{-1}}$.
The gravitational force acting on A is always in the downwards direction. Hence, there will be a change in velocity only in the vertical direction and the horizontal velocity will be constant.
Let the time taken for A to hit the ground be t. In this time, the particle is displaced by 20m downwards.
Let us use the kinematic equation $s=ut+\dfrac{1}{2}a{{t}^{2}}$ ……. (i),
where s, u and a are the displacement, initial velocity and acceleration of the particle. Apply the equation to the vertical motion of A.
In this case, s = -20, u = 0 and a = -g = -10$m{{s}^{-2}}$.
Substitute the values in equation (i).
$\Rightarrow -20=(0)t+\dfrac{1}{2}(-10){{t}^{2}}$
$\Rightarrow 20=5{{t}^{2}}$
$\Rightarrow {{t}^{2}}=4$.
$\Rightarrow t=2s$
The range of the A i.e. the horizontal distance moved by A is $R={{v}_{A}}t$.
$\Rightarrow R=12(2)=24m$.
Therefore, the range of particle A is 24m.

So, the correct answer is “Option A”.

Note: We can also find the range by using the other kinematic equation $2as={{v}^{2}}-{{u}^{2}}$, v is the velocity with which the particle hits the ground. Then we can substitute the value of v in the equation v = u + at to find the time of flight.