Question

Car A and B travels $100\,km$ journey together. Car A travels with uniform speed of $40\,kmh{r^{ - 1}}$ and Car B travels with $60\,kmh{r^{ - 1}}$ but after half an hour it stops for $15\min $ due to some problems and when it moves its speed remains $50\,kmh{r^{ - 1}}$
(a) Draw a speed time graph of journey
(b) Tell which car will complete the journey first and how much time before?

Answer 1

Hint: In order to solve this question we need to understand the difference between speed and velocity. Speed is a scalar quantity and it is mathematically defined as total distance covered per unit time whereas velocity is a vector quantity so it is defined as speed having some particular direction. Since speed is scalar quantity so two different speeds can be added linearly whereas velocity is a vector and two velocities can be added using the rule of vector addition.

Complete step by step answer:
Given the problem, Total journey distance is $d = 100\,km$.
Speed of a car A throughout the journey is ${v_1} = 40\,kmh{r^{ - 1}}$.
Let Speed of car B up to distance ${d_2}$ is ${v_2} = 60\,kmh{r^{ - 1}}$ in half hour and after $15\min $ speed to cover rest distance is ${v_3} = 50\,kmh{r^{ - 1}}$.
(a) Speed time journey can be drawn as:

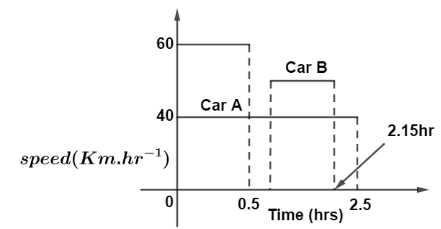
(b) Let the time taken by car A be ${t_1}$.
Therefore from definition of speed is, $v = \dfrac{d}{t}$
For Car A ${v_1} = \dfrac{{{d_1}}}{{{t_1}}}$
Putting values we get ${t_1} = \dfrac{{100}}{{40}}hr$
${t_1} = 2.5hr$
For Car B, distance up to speed is $60\,kmh{r^{ - 1}}$ be ${d_2}$ Since time taken to cover this distance is $t = 0.5hr$
Therefore, distance ${d_2}$ is given by ${v_2} = \dfrac{{{d_2}}}{t}$ or
${d_2} = {v_2} \times t$
Putting values we get ${d_2} = 60kmh{r^{ - 1}} \times 0.5hr$ or
${d_2} = 30km$
So distance left to cover for car B is ${d_3} = 100 - {d_2}$ Putting values we get
${d_3} = (100 - 30)km$ Or
$\Rightarrow {d_3} = 70\,km$

Since car B travels rest distance with speed ${v_3}$ let the time taken to travel this distance be ${t_2}$
So from speed formula we get ${v_3} = \dfrac{{{d_3}}}{{{t_2}}}$ or
${t_2} = \dfrac{{{d_3}}}{{{v_3}}}$
Putting values we get
${t_3} = \dfrac{{70}}{{50}}\,hr$
$\Rightarrow {t_3} = 1.4\,hr$
So total time taken for car B to travel distance is $t' = (t + (0.25) + {t_2})hr$
Here $0.25\,hr$ is time that car B stops
So Putting values we get
$t' = (0.5 + 0.25 + 1.4)\,hr$
$\Rightarrow t' = 2.15\,hr$
So Car A travels in time ${t_1} = 2.5\,hr$ and Car B travels in time $t' = 2.15\,hr$. So Car B travels faster than Car A. It reaches its destination earlier by $(2.5 - 2.15)hr = 0.35hr$.

Note:It should be remembered that we have considered here only translation motion not rotatory or any other. Translatory motion is defined as motion confined to only in one dimension, also known as straight line motion, so a force acting on the body in a straight line would either push or pull the body in the same dimension.