Question

Cannon A is located on a plain at distance L from a wall of height H. On top of this wall is an identical cannon (cannon B). Ignore air resistance throughout this problem. Also ignore size of cannons relative to L and H. The two groups of gunners aim the cannons directly at each other. They fire at each other simultaneously with equal muzzle speed\[{{v}_{0}}\]. What is the value of \[{{v}_{0}}\]for which the two cannonballs collide just as they hit the ground?

Answer 1

Hint: Here we have given a setup having two identical cannons which are facing each other. They fired by gunners on each other having equal muzzle speed. We have to find the velocity at which two balls collide at ground. To solve it, we will first draw the diagram and see the components of velocity and solve the question.
Formula used:
\[T=\dfrac{2u\sin \theta }{g}\]

Complete step by step answer:
Let us first draw a diagram for the given setup

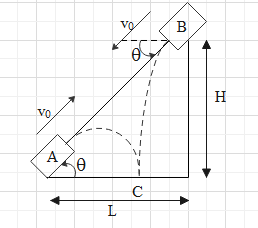
In the above figure two cannons are projected at each other and fired. The muzzle speed of both cannons are \[{{v}_{0}}\] and the distance of cannon A from wall is L and cannon B is situated at height H on the wall. Now due to gravitational pull it will have the trajectory and have a parabolic path. Let say the two cannon balls after being fired meet at point C and the velocity makes an angle θ with the plane. A simple diagram to show the components of speed can be given as follows

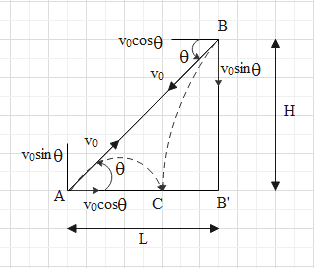
Now the time of flight for the projectile motion is given as
\[T=\dfrac{2u\sin \theta }{g}\]
Where u is the initial velocity, g is the acceleration due to gravity and θ is the angle between plane and velocity.
Now here the muzzle speed will be the initial speed with which the cannonballs are fired and the muzzle speed for both the cannon balls are same therefore the time of flight will be the same. Hence the time of flight for cannonballs fired from Cannon A and Cannon B, will be given as
\[T=\dfrac{2{{v}_{0}}\sin \theta }{g}\]
Now as we can see that AC plus AB’ will be equal to L. And AC can be given as speed multiplied by time, i.e. distance of AC is given as
\[\begin{align}
  & AC={{v}_{0}}\cos \theta \left( \dfrac{2{{v}_{0}}\sin \theta }{g} \right) \\
 & \Rightarrow AC=\dfrac{2v_{0}^{2}}{g}\left( \cos \theta \sin \theta \right) \\
\end{align}\]
Similarly distance of AB’ can be given as
By using AC and AB’, we can write
\[\begin{align}
  & L=AC+AB' \\
 & \Rightarrow L=\dfrac{2v_{0}^{2}}{g}\left( \cos \theta \sin \theta \right)+\dfrac{2v_{0}^{2}}{g}\left( \cos \theta \sin \theta \right) \\
 & \Rightarrow L=\dfrac{4v_{0}^{2}}{g}\left( \cos \theta \sin \theta \right) \\
 & \Rightarrow v_{0}^{2}=\dfrac{Lg}{4\cos \theta \sin \theta }\text{ }........\text{(i)} \\
\end{align}\]
As we have assumed θ, therefore we have to represent it in terms of L and H.
By using trigonometry, we know that
 \[\begin{align}
  & \cos \theta =\dfrac{\text{height}}{\text{hypotenuse}} \\
 & \sin \theta =\dfrac{\text{base}}{\text{hypotenuse}} \\
\end{align}\]
Here height is H, base is L and hypotenuse will be
\[\begin{align}
  & \text{hypotenuse=}\sqrt{{{\left( \text{height} \right)}^{2}}\text{+}{{\left( \text{base} \right)}^{2}}} \\
 & \text{hypotenuse=}\sqrt{{{\left( H \right)}^{2}}\text{+}{{\left( L \right)}^{2}}} \\
\end{align}\]
Hence value of cos θ and sin θ will be given as
\[\begin{align}
  & \cos \theta =\dfrac{H}{\sqrt{{{\left( H \right)}^{2}}\text{+}{{\left( L \right)}^{2}}}} \\
 & \sin \theta =\dfrac{L}{\sqrt{{{\left( H \right)}^{2}}\text{+}{{\left( L \right)}^{2}}}} \\
\end{align}\]
Substituting this value of sin θ and cos θ in equation (i), we get
\[\begin{align}
  & v_{0}^{2}=\dfrac{Lg}{4\left( \dfrac{H}{\sqrt{{{\left( H \right)}^{2}}\text{+}{{\left( L \right)}^{2}}}} \right)\left( \dfrac{L}{\sqrt{{{\left( H \right)}^{2}}\text{+}{{\left( L \right)}^{2}}}} \right)} \\
 & \Rightarrow v_{0}^{2}=\dfrac{Lg}{4\dfrac{LH}{\left( {{L}^{2}}+{{H}^{2}} \right)}} \\
 & \Rightarrow v_{0}^{2}=\dfrac{\left( {{L}^{2}}+{{H}^{2}} \right)g}{4H} \\
 & \Rightarrow {{v}_{0}}=\sqrt{\dfrac{\left( {{L}^{2}}+{{H}^{2}} \right)g}{4H}} \\
 & \Rightarrow {{v}_{0}}=\dfrac{1}{2}\sqrt{\dfrac{\left( {{L}^{2}}+{{H}^{2}} \right)g}{H}} \\
\end{align}\]
Hence we got an equation for muzzle speed in terms of H, L and g.

Note:
Here we have ignored air resistance. In case we have considered it, then the balls would have not reached at point C, due to air resistance it would have landed before the point C. So the balls from both cannons wouldn't collide. They would have landed at some distance apart from each other.