Question

Can we have rotational symmetry of order more than 1 if whose angle of rotation is \[17{}^\circ \] ?

Answer 1

Hint: We have to understand meaning of rotational symmetry which is given as the number of times a shape can be rotated around full circle i.e. \[360{}^\circ \] and we can find out how many time shape looks like original shape. That number will be the order of rotational symmetry. Then, we can find out whether the given angle is a factor of \[360{}^\circ \] or not. If yes, then order will be more than 1.

Complete step-by-step solution -
Here, first we have to understand what is meant by rotational symmetry.
Rotational Symmetry means how many times a shape is rotated around a full circle but still looks the same every time. This number obtained is called order of rotation. All the shapes have a minimum order of 1 i.e. its original shape.
Now, we will take an example to understand this.

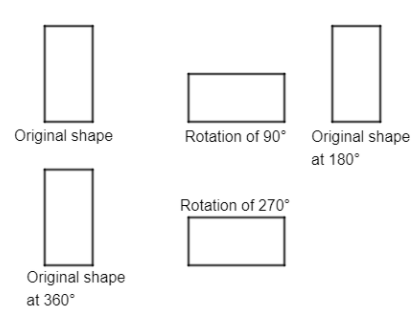
Here, we have taken a rectangle whose angle of rotation is \[90{}^\circ \]. So, we have the first image as an original image. After making the rotation of \[90{}^\circ \] as we can see, the image is not the same as the original shape. Then again after rotation of \[90{}^\circ \] i.e. $180{}^\circ$, the shape is in its original form. Similarly, at $270{}^\circ$ it is not in its original form and then last at \[360{}^\circ \], it is in its original form.
So, here the original shape occurs 2 times i.e. \[180{}^\circ \] and \[360{}^\circ \]. So, the order of rotational symmetry is 2.
Now, here we are asked to find the order of rotational symmetry whose angle of rotation is \[17{}^\circ \].
We know that summation of all the angles of any shape is equal to \[360{}^\circ \]. So, the angle of rotation will be a factor of \[360{}^\circ \]. As seen in the above example, rotation is made of \[90{}^\circ \] which is factor of \[360{}^\circ \] i.e. \[\dfrac{360}{90}=4\].
Similarly, \[17{}^\circ \] is not a factor of \[360{}^\circ \]. We can see the factors of \[360{}^\circ \] are \[2,3,4,5,6,8,9,10,12,15,18,20,45,60,...\] So on. We can not note down all the factors here. But we can see from the list that 17 is not a factor.
So, here 17 cannot divide 360 with remainder 0. Therefore, the order of rotational symmetry is not more than 1.
Thus, we cannot have rotational symmetry of order more than 1 if whose angle of rotation is \[17{}^\circ \].

Note: Do not confuse the rotational symmetry and plane symmetry. Plane symmetry means only we have to draw a line in such a way that shape can be equally divided. While in rotational symmetry we have to rotate shape at any given angle and then find out the order of it. Also, while counting the order do not consider the original shape into it otherwise order will be always +1 and the answer will go wrong. So, do not make counting mistakes.