Question

Can two acute angles be vertical, adjacent, complementary, or supplementary?

Answer 1

Hint: In such types of questions always remember the condition of vertical, adjacent, complementary and supplementary angles respectively. Vertical angles are always equal to one another, then supplementary angles have total of \[{180^ \circ }\] and then complementary angles have total which is half of the total of all the supplementary angles. We know that acute angles are less than 90 degrees. And so by using all these points, we can easily find out the final output.

Complete step by step answer:
We know that,acute angles, by definition, are angles that measure greater than \[{0^ \circ }\]and less than \[{90^ \circ }\], or \[{0^ \circ } < \theta < {90^ \circ }\]. Also, supplementary angles, by definition, are positive angles that add up to \[{180^ \circ }\]. Complementary angles are two angles with measures x and y, such that \[x\; + \;y\; = {90^ \circ }\]. An acute angle is any angle that has a measure that is less than \[{90^ \circ }\] .

First, we will check if vertical angles are acute or not: Vertical angles are always equal to one another. In general, we can say that 2 pairs of vertical angles are formed when two lines intersect. Vertical angles are supplementary angles when the lines intersect perpendicularly.

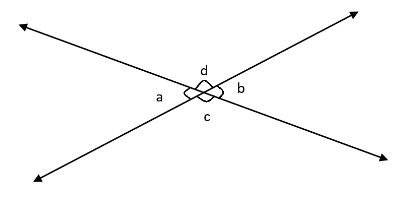
Two angles \[\angle a\] and \[\angle b\] are vertical angles and are acute too (smaller than \[{90^ \circ }\]). Similarly two angles \[\angle c\] and \[\angle d\] are vertical angles too.

Second, we will check if adjacent angles are acute or not: The two angles are said to be adjacent angles when they share the common vertex and side.

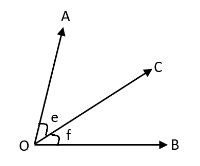
\[\angle AOC\] and \[\angle COB\] have a common vertex, a common arm and the uncommon arms lie on either side of the common arms. Such angles are known as adjacent angles. Here, angles \[\angle e\] and \[\angle f\]are adjacent (share one side) and also acute angles too.

Next, will check for complementary angles are acute or not:

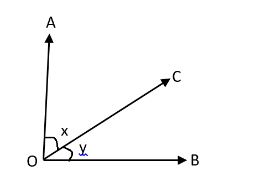
Angles \[\angle x\] and \[\angle y\]are complementary angles and also acute angles too.

Lastly, we will check if supplementary angles are acute or not:

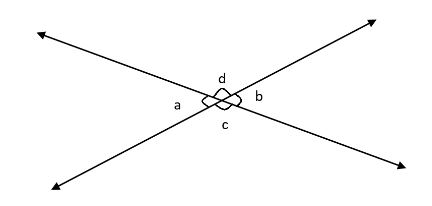
Here, \[\angle b\] and \[\angle c\] are supplementary angles. Their sum must be \[{180^ \circ }\]to be supplementary, but it will be less than \[{180^ \circ }\]because each acute angle is less than \[{90^ \circ }\]. Thus, two acute angles cannot be supplementary because each of them is smaller than \[{90^ \circ }\].

Hence, two acute angles can be vertical, adjacent and complementary but not supplementary.

Note: We can also say that the two vertical angles share a common vertex (the common endpoint of two or more lines or rays). Adjacent angles can be a complementary angle or supplementary angle when they share the common vertex and side. If the two supplementary angles are adjacent to each other then they are called linear pairs. Then the sum of the adjacent supplementary angles is 180 degrees.