Question

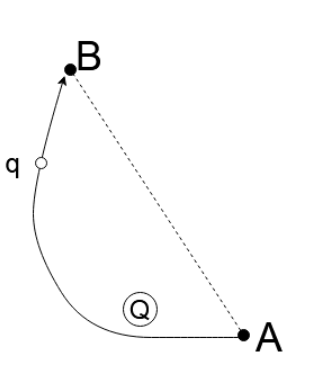
Calculate the work done by the electric field when a point charge $q$ is moved from point $B$ to $A$ along the curved path. Given that the electric field is created by the stationary charge $Q$ and ${V_A} = 200V$ , ${V_B} = 100V$ , $q = 0.05C$ , length of the line segment $AB = 10cm$ , the length of the curved path $ = 20cm$ .

 (A). $0J$
 (B). $5J$
 (C). $10J$
 (D). $15J$
 (E). $20J$

Answer 1

Hint: You can start by discussing conservative fields. Remember to explain how work is done in a conservative field independent of the path taken. Then move to explain the electric potential and the work is done in an electric field. Then use the equation $W = qV$ to calculate the work done.

Complete step-by-step answer:
Conservative fields – Conservative vector fields have a peculiar property. The line integral in a conservative field is independent of the path chosen between two points.
In the case of electric fields, it simply means that the work done in moving a charge from one point to another is independent of the path taken for moving the charge.
Electric potential – It is a scalar quantity. The electric potential on a point in an electric field is the work done in bringing a unit charge from infinity to that point.
Work - It is the work done in moving a charge $q$ from infinity to a distance $r$ in the electric field.
We know that the work done by an electric field is
$W = qV$
Here, $W = $ Work done
$q = $ The magnitude of the charge
$V = {V_A} - {V_B} = $ The difference in the electric potential between the two points
So,
$W = 0.05(200 - 100) = 5J$
Hence, option B is the correct answer.

Note: The work done in an electric field is stored in the charge as potential energy. Work is done in an electric field to move the charge against the force of attraction and repulsion applied to the charge by the electric field. This work done is only dependent on the initial and final position of the charge and the magnitude of the charge.