Question

Calculate the work done by a coolie in carrying a load of mass $10kg$ on his head when he walks uniformly a distance of $5m$ in the (i) Horizontal direction (ii) Vertical direction (take $g = 10m{s^{ - 2}}$)
A) 500,0
B) 0,500
C) 1,500
D) 500,3

Answer 1

Hint:Work done on an object or by an object is the amount of force that displaces it by unit displacement. Or we can say that if there is no displacement at all, no matter what amount of force we put, the net work done will be zero. Horizontal work means, work done along the x-axis and vertical work done means along the y-axis in our frame of reference.

Complete step by step answer:
Work done on an object or by an object is simply the force expended to displace it for a certain displacement. Mathematically it is defined as the scalar product or dot product of expended force and resulting displacement.
$W = \overrightarrow F \cdot \overrightarrow s $
$ \Rightarrow W = Fs\cos \theta $
Where $W$ is the work done for a displacement of $s$ by the force $F$
In the given problem, the coolie is carrying a load of $10kg$ over his head and moving in a horizontal displacement of $5m$ .
In horizontal displacement, force is expended by the coolie along the y-axis and the displacement vector is along the x-axis as shown in the following diagram.

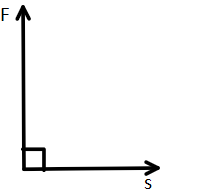
Thus the work done is given by
$ \Rightarrow W = Fs\cos 90^\circ $
Putting the value of $\cos 90^\circ $ , this work done is zero.
This answers (i)
Now, if the vertical displacement, the coolie has worked against acceleration due to gravity and displaced the box $5m$ upwards along the direction of force that is along the y-axis.
So work done in vertical displacement is given by
$ \Rightarrow W = Fs\cos 0^\circ $
Now we know from Newton’s second law,
$F = mg$
Putting the respective values of terms in the above equation we get, $F = 100N$
Now substituting the value of force and vertical displacement in the expression of vertical work done, we get
$ \Rightarrow W = 500J$
This answers (ii)

So the correct selection is, option B.

Note:If the net displacement turns out to be zero when solving a problem, the work done will also be zero. There are often questions asked with application of this trick. One should know the use of frame of reference and resolving vectors along axes. And also, don’t forget to check the system of units.