Question

Calculate the value of $\underset{z\in S}{\mathop{\min }}\,\left| 1-3i-z \right|=$ such that $\text{S}={{\text{S}}_{1}}\cap {{\text{S}}_{2}}\cap {{\text{S}}_{3}}$ where ${{\text{S}}_{1}}=\left\{ z\in C:\left| z \right|<4 \right\}$, ${{\text{S}}_{2}}=\left\{ z\in C:\operatorname{Im}\left[ \dfrac{z-1+\sqrt{3}i}{1-\sqrt{3}i} \right]>0 \right\}$ and ${{\text{S}}_{3}}=\left\{ z\in C:\operatorname{Re}Z>0 \right\}$ .
A. $\dfrac{2-\sqrt{3}}{2}$
B. $\dfrac{2+\sqrt{3}}{2}$
C. $\dfrac{3-\sqrt{3}}{2}$
D. $\dfrac{3+\sqrt{3}}{2}$

Answer 1

Hint: For this problem we need to calculate the minimum value of the given expression. In the problem we need to have the additional information that $\text{S}={{\text{S}}_{1}}\cap {{\text{S}}_{2}}\cap {{\text{S}}_{3}}$ where ${{\text{S}}_{1}}=\left\{ z\in C:\left| z \right|<4 \right\}$, ${{\text{S}}_{2}}=\left\{ z\in C:\operatorname{Im}\left[ \dfrac{z-1+\sqrt{3}i}{1-\sqrt{3}i} \right]>0 \right\}$ and ${{\text{S}}_{3}}=\left\{ z\in C:\operatorname{Re}Z>0 \right\}$. From this data we will calculate the range of the variable $z$ by substituting the value $z=x+iy$. Now we will calculate the perpendicular distance from the point $\left( -1,3 \right)$ and the region to get the required result.


Complete step by step solution:
Given that, $\text{S}={{\text{S}}_{1}}\cap {{\text{S}}_{2}}\cap {{\text{S}}_{3}}$ where ${{\text{S}}_{1}}=\left\{ z\in C:\left| z \right|<4 \right\}$, ${{\text{S}}_{2}}=\left\{ z\in C:\operatorname{Im}\left[ \dfrac{z-1+\sqrt{3}i}{1-\sqrt{3}i} \right]>0 \right\}$ and ${{\text{S}}_{3}}=\left\{ z\in C:\operatorname{Re}Z>0 \right\}$.
Considering ${{\text{S}}_{1}}=\left\{ z\in C:\left| z \right|<4 \right\}$. Here we have that $\left| z \right|<4$. Substituting the value $z=x+iy$ in the above expression, then we will get
$\begin{align}
  & \left| z \right|<4 \\
 & \Rightarrow \left| x+iy \right|<4 \\
\end{align}$
We know that the modulus of the complex number $a+ib$ is given by $\left| a+ib \right|=\sqrt{{{a}^{2}}+{{b}^{2}}}$. Using this formula in the above equation, then we will get
$\sqrt{{{x}^{2}}+{{y}^{2}}}<4$
Squaring on both sides of the above expression, then we will get
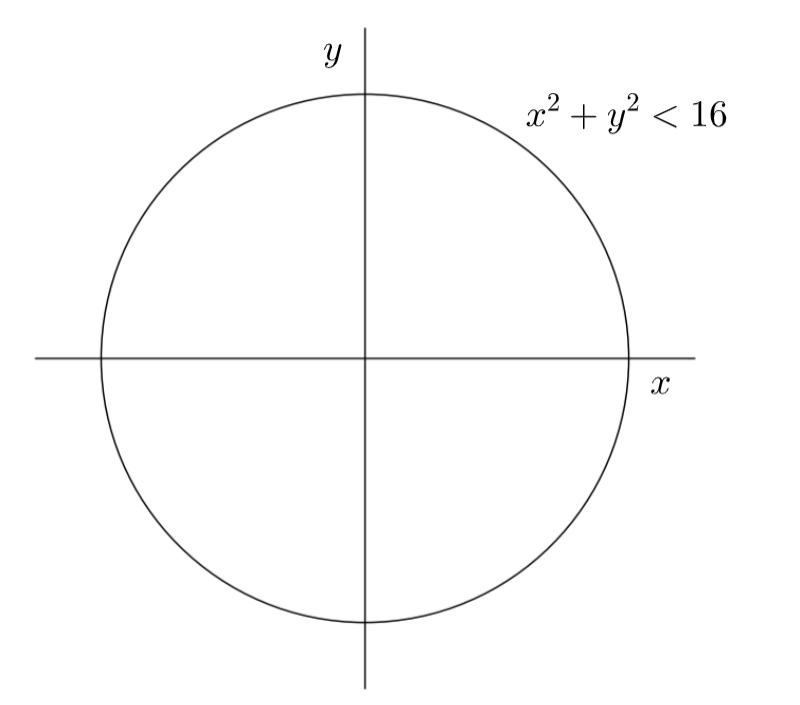
${{x}^{2}}+{{y}^{2}}<16$
Now the graph of the expression ${{x}^{2}}+{{y}^{2}}<16$ will be

Now considering ${{\text{S}}_{2}}=\left\{ z\in C:\operatorname{Im}\left[ \dfrac{z-1+\sqrt{3}i}{1-\sqrt{3}i} \right]>0 \right\}$. In the above equation we have the value
$\begin{align}
  & \operatorname{Im}\left[ \dfrac{z-1+\sqrt{3}i}{1-\sqrt{3}i} \right]>0 \\
 & \Rightarrow \operatorname{Im}\left[ \left( x+iy-1+i\sqrt{3} \right)\left( 1+i\sqrt{3} \right) \right]>0 \\
 & \Rightarrow y+\sqrt{3}x>0 \\
 & \Rightarrow {{\text{S}}_{2}}=\left\{ z\in C:y+\sqrt{3}x>0 \right\} \\
\end{align}$
Now the graph of the given data will be as shown in below

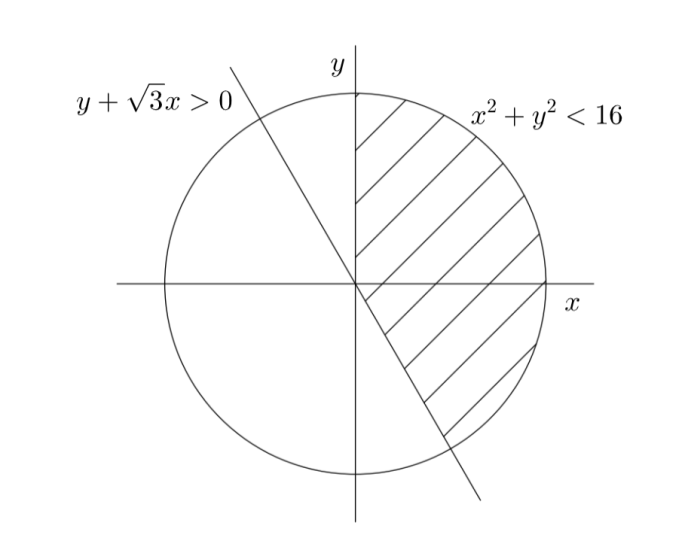
Now the minimum distance between point $P\left( -1,3 \right)$ and region $\text{S}$, which is perpendicular distance from point $P\left( -1,3 \right)$ to straight line $y+\sqrt{3}x=0$
$\begin{align}
  & \therefore \underset{z\in S}{\mathop{\min }}\,\left| z-1+3i \right|=\left| \dfrac{\left( -3 \right)+\sqrt{3}\left( 1 \right)}{\sqrt{{{1}^{2}}+{{\left( \sqrt{3} \right)}^{2}}}} \right| \\
 & \Rightarrow \underset{z\in S}{\mathop{\min }}\,\left| z-1+3i \right|=\dfrac{3-\sqrt{3}}{2} \\
\end{align}$
Hence option ‘C’ is correct.

Note:
For this problem we have evaluated the range of the variable $z$ from each given set one by one by using graphical representations. We can also directly estimate the range of the variable $z$ by using the given sets and calculate the required value.