Question

Calculate the smaller force if the bigger force is \[40N\] and the resultant force is perpendicular to the smaller force. The two forces are acting at an angle of \[{120^0}\].

Answer 1

Hint: Vectors add according to the triangle law or equivalent parallelogram. Let the resultant force be \[R\]. This vector is making a right angle with a smaller force\[{\vec F_1}\]. This implies that the resultant makes an angle \[{30^0}\] with a bigger force \[{\vec F_2}\].
Diagram:
     

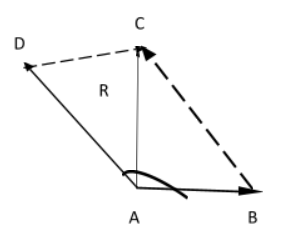
Complete answer:
Let the smaller force be represented by \[{\vec F_1}\] and the bigger force be represented by \[{\vec F_2}\]
From the right angle triangle ACD, defining \[\sin \alpha \] we get
\[\sin \alpha = \dfrac{{{\text{Opposite}}}}{{Adjacent}} = \dfrac{{DC}}{{AD}}\]
We know that \[AD\]=\[{\vec F_2}\]=\[40N\]
The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure. Also opposite sides of the parallelogram are equal. Therefore
\[DC\]=\[AB\]=\[{\vec F_1}\]=?
By parallelogram law of vectors, the resultant force be represented by \[{\vec F_R}\]
We know that \[\left| \!{\underline {\,
  {DAB} \,}} \right. = {120^0}\], therefore
\[\left| \!{\underline {\,
  {DAC} \,}} \right. = {120^0} - {90^0} = {30^0}\]
\[\sin {30^0} = \dfrac{{{{\vec F}_1}}}{{{{\vec F}_2}}}\]
\[{\vec F_1}\]=\[\sin {30^0} \times {\vec F_2}\]
\[{F_1} = \dfrac{1}{2} \times 40\]
\[{F_1} = 20N\]
Therefore the smaller force is \[20N\].

Note:
This problem may also be solved using another method.
Let there be two vectors \[\vec A{\text{ and }}\vec B\]
Let the angle \[\theta = {120^0}\] between the two vectors. We know the resultant force formula as
\[R.F = \sqrt[2]{{{F_1}^2 + {F_2}^2 + 2{F_1}{F_2}\cos \theta }}\]
Here, \[R.F\] is the resulting force
\[{F_1}\] and \[{F_2}\] are the known two forces
\[\theta \] is the angle between the two forces.
\[{\left| {RF} \right|^2} = {\left| A \right|^2} + {\left| B \right|^2} + 2AB\cos \theta \]
Let A be the bigger force and B be the smaller force.
We know that \[\theta = {120^0}\], substituting in the above formula,
Value for \[\cos {120^0} = - \dfrac{1}{2}\],
\[R{F^2} = {A^2} + {B^2} - AB\]
Given that the resultant makes a right angle with the smaller force
So \[B = - A\cos \theta \]---- (1)
Substituting the known values that are,
\[{\rm A} = 40{\rm N}\]
\[\theta = 12{0^0}\]
Substituting in equation 1 we get,
\[B = - 40 \times - \dfrac{1}{2}\]
\[B = 20N\]
Thus we can also use this method to find the smaller force.