Question

Calculate the lattice energy of a salt \[MX(s)\]​ from the date given below:
Heat of formation of \[MX\left( {\Delta H} \right)\; = - 550\;kJ/mol\]
Heat of sublimation of \[M\left( S \right) = 80\;kJ/mol\]
Heat of dissociation of \[{X_2}\left( D \right) = 155\;kJ/mol\]
Ionization energy of \[M\left( {IE} \right) = 347\;kJ/mol\]
Electron affinity of \[X\left( {EA} \right) = - 343\;kJ/mol\]
A. \[ - 835KJ/mol\]
B. \[ - 938.5{\text{ }}kJ/mol\]
C. \[ - 711.5{\text{ }}kJ/mol\]
D. \[ - 638.5{\text{ }}kJ/mol\]

Answer 1

Hint:Born Haber cycle is mainly used to calculate the lattice energy. It also involves steps such as sublimation energy \[\left( {\Delta {H_{sub}}\;} \right),\] dissociation energy \[\left( D \right),\] ionisation energy\[\left( I \right),\] electron affinity\[\left( E \right)\] and heat of formation of crystal \[\left( H \right).\] Represented in the form of
\[\Delta {\text{ }}H{\;_{f{\;^0}}}\; = {\text{ }}\Delta H\;sub\; + {\text{ }}\dfrac{D}{2} + {\text{ }}IE{\text{ }} + {\text{ }}EA\; + U\]

Complete step by step answer:
Born Haber cycle is a cycle of enthalpy change of process and The energy terms involved in building a crystal lattice\[\left( {{\text{ }}MX} \right)\] such as -
Step\[\;1\] - convert solid \[\left( {{\text{ }}M} \right)\] to gaseous \[\left( {{\text{ }}M} \right)\]is called enthalpy of sublimation \[\left( {\Delta H\;sub} \right).\]
 Step \[2\] - convert gaseous\[\left( X \right)\] molecule to atoms is called enthalpy of dissociation\[\left( D \right).\]
Step \[3\] - Conversion of gaseous \[\left( {{\text{ }}M} \right)\] atom into \[\left( {M{\text{ }}ion} \right)\] in gaseous state is called ionisation energy .
Step \[4\] - Conversion of gaseous \[\left( X \right)\] atom into gaseous \[X{\text{ }}\;ion\] is known as electron gain enthalpy and represented by \[{E_A}\;.\]
Step \[5\] - The amount of energy released when one mole of solid crystalline compound is obtained from gaseous ions is called lattice energy\[\left( U \right)\]
   \[M\left( s \right) + {\text{ }}\dfrac{1}{2}X\;\left( g \right) \to MX\left( s \right)\]
The Born-Haber Cycle can be reduced to a single equation:
Heat of formation= Heat of atomization + Dissociation energy+ (sum of Ionization energies) + (sum of Electron affinities)+ Lattice energy

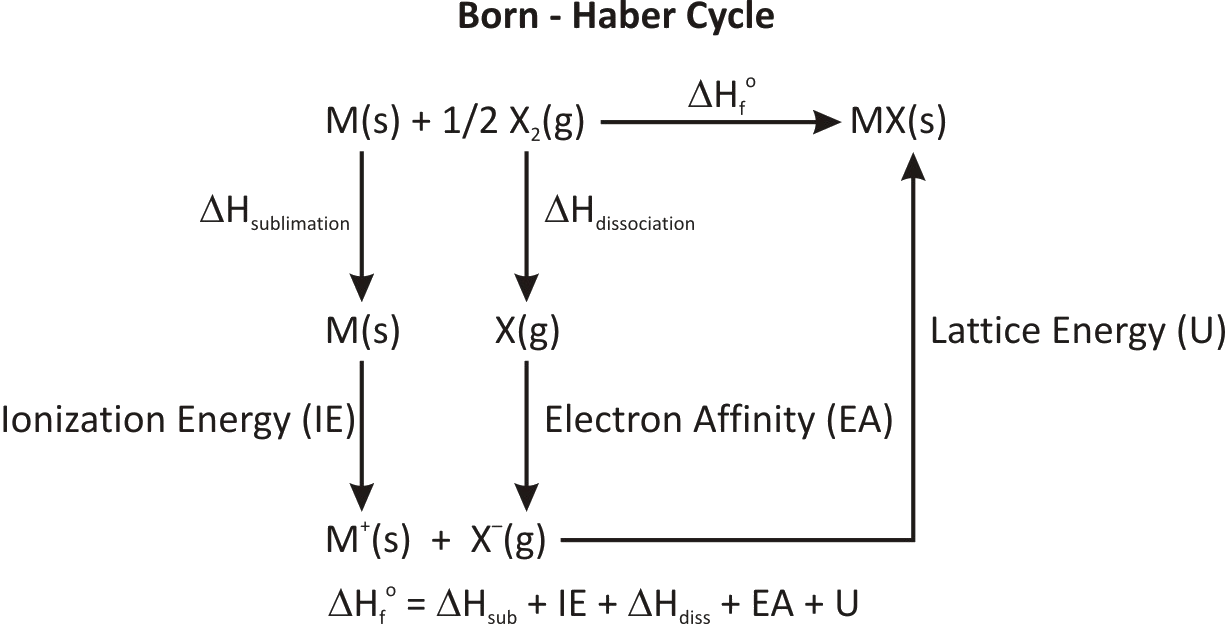
The enthalpies are represented in figure.
These steps are represented as -
\[\Delta {\text{ }}H{\;_f}^0\; = {\text{ }}\Delta H{\;_{sub}}\; + {\text{ }}D/2{\text{ }} + {\text{ }}IE{\text{ }} + {\text{ }}{E_A}\; + U\]
 Now, Putting values as -
   \[\Delta {H_f}\; = \;\;\;S{\text{ }} + {\text{ }}0.5D{\text{ }} + {\text{ }}IE{\text{ }} + {\text{ }}EA{\text{ }} + {\text{ }}U\]
  \[ - 550{\text{ }} = \;\;80 + \dfrac{{155}}{2} + 347 - 343 + U\]
\[\;\;U = - 711.5kJ/mol\]
 lattice energy of salt \[ = \; - 711.5\;kJ/mol.\]
Option (c ) is correct.
Note:Born Haber process is a method that allows us to observe and analyze energies in a reaction. It mainly helps in describing the formation of ionic compounds from different elements. Born Haber cycle is a process that leads to the formation of a solid crystalline ionic compound from the elemental atoms in their standard state and of the enthalpy of formation of the solid compound such that the net enthalpy becomes zero.