Question

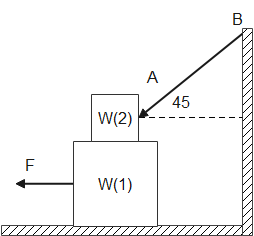
Calculate the force F required to cause the block of weight ${{W}_{1}}=200N$ just to slide under the block of weight ${{W}_{2}}=100N$. What is the tension in the string AB? [Coefficient of friction $\mu $=0.25 for all surfaces in constant].
          

Answer 1

Hint: In this question we will also be using newton’s third law of motion which is also known as action reaction, this law states that every action has an equal and opposite reaction. This law deals with the direction too. Since it states that there will be equal and also opposite reactions. Opposite means that the direction will be opposite.

Complete answer:
In the question we have been given with two blocks and coefficient of friction, The given quantities are as follows
Weight of block 1 is ${{W}_{1}}=200N$
Weight of Block 2 is ${{W}_{2}}=100N$
Coefficient of friction $\mu $=0.25
Additionally, we have given an angle which is equal to ${{45}^{\circ }}$
Now we know that the force of friction can be given as
${{F}_{f}}=\mu N$
Where ${{F}_{f}}$is the frictional force and N is the normal force or normal reaction.
$\mu $ is the coefficient of friction
Now Normal reaction will be equal to the weight of the object as there is no other force acting in downward or upward direction
So, ${{N}_{1}}={{W}_{1}}$ and ${{N}_{2}}={{W}_{2}}$
But as shown in the above figure the frictional force on the lower block or 1st block will be due to the weight of both the blocks. So,
${{F}_{1}}=\mu ({{W}_{1}}+{{W}_{2}})$
Where ${{F}_{1}}$ is the frictional force due on block 1 or on lower block
While in case of upper or 2nd block the force will be only due to weight of 2nd block
${{F}_{2}}=\mu {{W}_{2}}$
Where ${{F}_{2}}$ is the frictional force due to the 2nd block.
Now the total force will be
$F={{F}_{1}}+{{F}_{2}}$
$F=\mu ({{W}_{1}}+{{W}_{2}})+\mu {{W}_{2}}$
Now putting the values in above equation, we get
$F=0.25(200+100)+0.25(100)$
$F=100N$
Hence 100 N of force is required to slide the block
Now in the question we have been asked about the tension in the string
So, by using newton's third law we get,
$F=-T$
Therefore (-100N) of tension will be there in the string

Note:
In the answer, we have negative signs. Negative sign in the value of tension denotes the direction, it does not mean that the force will be negative. The negative sign indicates that the tension will act in the opposite direction as that of force. Which is absolutely correct and satisfies newton’s third law of motion