Question

Calculate the following in a triangle ABC, D is the midpoint of AB and E is the midpoint of AC. \[\]
i)DE if BC=8cm\[\]
ii)$\angle ADE$ if $\angle DBC={{125}^{\circ }}$\[\]
b)If $\dfrac{{{9}^{n}}{{.3}^{2}}\cdot {{3}^{n}}{{27}^{n}}}{{{2}^{3m}}}=\dfrac{3}{8},$Find the value of $m-n$ where $m,n$ are integers. \[\]

Answer 1

Hint: We prove the similarity of triangles ADE and ABC in part(a). We use the ratio of sides to get DE. We use the equality of corresponding angles to get $\angle ADE$. We prime factorize 9 and 27 in the second part(b) and use identities like ${{\left( {{a}^{m}} \right)}^{n}}={{a}^{mn}}$,${{\left( {{a}^{m}} \right)}^{n}}={{a}^{mn}}$ to get an expression. We check for which integral values of $x$ the equation satisfies.

Complete step-by-step solution:
(a) We have the triangle ABC , D is the midpoint o f AB and E is the midpoint of AC , $AD=DB,AE=EB$ So we have
\[\begin{align}
  & AB=AD+DB=AD+AD=2AD \\
 & AC=AE+EC=AE+AE=2AE \\
\end{align}\]
 

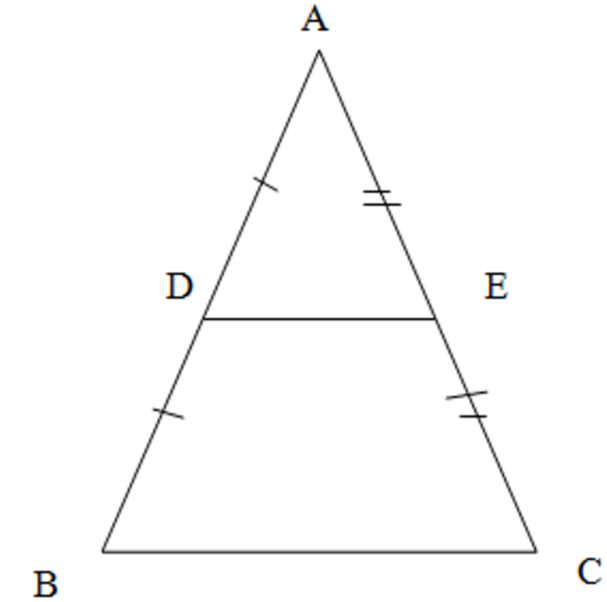
We have joined DE. . We know that lie joining the midpoints two sides will be parallel to the other side. So $DE||BC$. \[\]
 We observe the triangles ADE and ABC. We have corresponding angles formed by the line AB cutting the parallel lines DE and BC . They will be equal. So we have $\angle ABC=\angle ADE$ . Similarly AC cuts the parallel lines DE and BC and makes equal corresponding angles$\angle AED=\angle ACB$. The angle $\angle BAC=\angle DAE$ is the common angle to both the triangles. So use angle-angle-angle similarity to conclude triangles $\Delta ADE\sim \Delta ABC$
So the sides will be in equal ratio which means
\[\begin{align}
  & \dfrac{AD}{AB}=\dfrac{AE}{AC}=\dfrac{DE}{BC} \\
 & \Rightarrow \dfrac{AD}{2AD}=\dfrac{AE}{2AE}=\dfrac{DE}{BC} \\
 & \Rightarrow \dfrac{1}{2}=\dfrac{1}{2}=\dfrac{DE}{BC} \\
 & \Rightarrow DE=\dfrac{1}{2}BC \\
\end{align}\]
 (i)We are given that BC=8cm. So we find $DE=\dfrac{1}{2}BC=\dfrac{1}{2}\times 8=4$cm.
(ii) We are given $\angle DBC={{125}^{\circ }}$. So we have by corresponding angles $\angle ADE=\angle DBC={{125}^{\circ }}$ \[\]
(b) We are given
$\dfrac{{{9}^{n}}{{.3}^{2}}\cdot {{3}^{n}}-{{27}^{n}}}{{{2}^{3m}}}=\dfrac{1}{8},$
We proceed by replacing the composite numbers 9 and 27 by their prime factorization.
\[\begin{align}
  & \dfrac{{{\left( 3\times 3 \right)}^{n}}{{.3}^{2}}{{.3}^{n}}-{{\left( 3\times 3\times 3 \right)}^{n}}}{{{2}^{3m}}}=\dfrac{1}{8} \\
 & \Rightarrow \dfrac{{{\left( {{3}^{2}} \right)}^{n}}{{.3}^{2}}{{.3}^{n}}-{{\left( {{3}^{3}} \right)}^{n}}}{{{2}^{3m}}}=\dfrac{1}{8} \\
\end{align}\]
We use the formula ${{\left( {{a}^{m}} \right)}^{n}}={{a}^{mn}}$ where $a,m,n$ are real numbers and get
\[\Rightarrow \dfrac{{{3}^{2n}}{{.3}^{2}}{{.3}^{n}}-{{3}^{3n}}}{{{2}^{3m}}}=\dfrac{1}{8}\]
We use the formula ${{a}^{m}}\cdot {{a}^{n}}={{a}^{m+n}}$ and get
\[\begin{align}
  & \Rightarrow \dfrac{{{3}^{3n+2}}-{{3}^{3n}}}{{{2}^{3m}}}=\dfrac{1}{8} \\
 & \Rightarrow \dfrac{{{3}^{3n}}{{.3}^{2}}-{{3}^{3n}}}{{{2}^{3m}}}=\dfrac{1}{8} \\
 & \Rightarrow \dfrac{{{3}^{3n}}\left( 9-1 \right)}{{{2}^{3m}}}=\dfrac{1}{8} \\
 & \Rightarrow \dfrac{{{3}^{3n}}}{{{2}^{2m}}}=\dfrac{1}{8\times 8}=\dfrac{1}{64} \\
\end{align}\]
The above result is true when for integral values of $m,n$. The above is result true when ${{3}^{3n}}=1={{3}^{0}}$. Equating exponent we get $n=0$. Similarly we have ${{2}^{2m}}=64={{2}^{6}}$ and by equating exponents we get $m=3$. So the asked result is $m-n=3-0=3$\[\]

Note: We need to take care of confusion of similarity from congruence which is the equality of angles and sides of two different triangles. We can only find a non-integral solution when the base of the exponents $m,n$ are the same. We take care of the fact when we use the formula ${{\left( {{a}^{m}} \right)}^{n}}={{a}^{mn}}$ that both $a$ and $m$ are not zero at the same time.